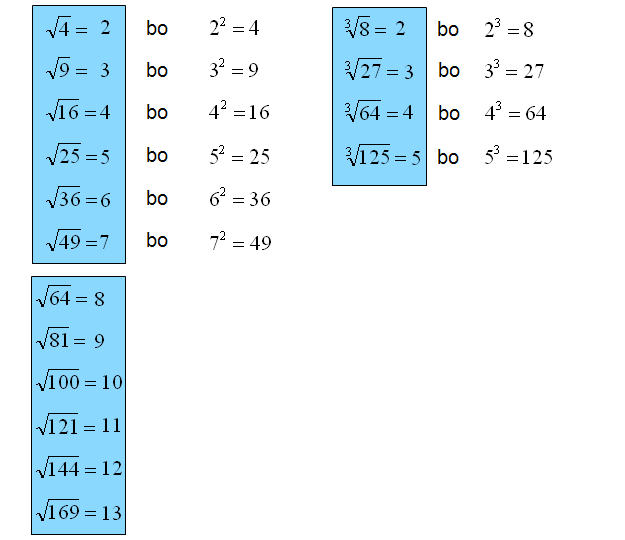Wykonując działanie: pierwiastek z potęgi pamiętaj, że głównym wzorem jest tutaj: Zauważ, że w miejsce literki x pod pierwiastkiem możesz wstawić zarówno liczbę dodatnią i ujemną i zawsze wynik będzie dodatni. Potęga parzysta pod pierwiastkiem sprawia, że podstawa pierwiastka będzie zawsze dodatnia. Wzór można uprościć do , gdy x≥0. Potęgi i pierwiastki - najważniejsze wzory W tym miejscu znajduje się zestawienie najważniejszych wzorów z działań na potęgach i pierwiastkach. Przykłady zastosowania tych wzorów znajdziesz w kolejnych rozdziałach. Definicja potęgi o wykładniku naturalnym an = a ⋅ a ⋅ a⋅. ⋅a n razy Wzory na potęgi o wykładnikach wymiernych

Pierwiastkowanie i pierwiastki Wstęp Matfiz24.pl YouTube
Pierwiastek z liczby obliczamy tak, że szukamy liczby, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem. Przykład 1. a) 4-√ = 2, ponieważ 22 = 4 b) 9-√ = 3, ponieważ 32 = 9 c) 49−−√ = 7, ponieważ 72 = 49 d) 1 16−−−√ = 1 4, ponieważ (1 4)2 = 1 16 e) 25 81−−−√ = 5 9, ponieważ (5 9)2 = 25 81 Pierwiastki Potęgowanie pierwiastków W poprzednich częściach zajmowaliśmy się potęgowaniem i pierwiastkowaniem liczb. Teraz, dzięki umiejętności zapisywania pierwiastka za pomocą potęgi, połączymy oba te działania. W jaki sposób? Na początku spójrz na przykład. Weźmy liczbę (√16)2. Chcemy ją jakoś policzyć. Jak? Są na to 2 sposoby: Sposób I. Podnoszenie potęgi do potęgi. 8. Potęga o wykładniku 0. 9. Potęga o wykładniku ujemnym. 10. Pierwiastkowanie. 11. Potęga o wykładniku wymiernym. 12. Zadania z potęgowania i pierwiastkowania. Potęgi i pierwiastki - najważniejsze wzory. W tym miejscu znajduje się zestawienie najważniejszych wzorów z działań na potęgach i. Rozdział 7 Liczby ujemne i układ współrzędnych. Rozdział 8 Stosunki i proporcje. Rozdział 9 Wyrażenia, równania i nierówności. Rozdział 10 Potęgi, pierwiastki i notacja naukowa. Wyzwanie. Sprawdź swoje umiejętności w zakresie objętym tą ścieżką. Zacznij wyzwanie z kursu. Matematyka. Wstęp do algebry.
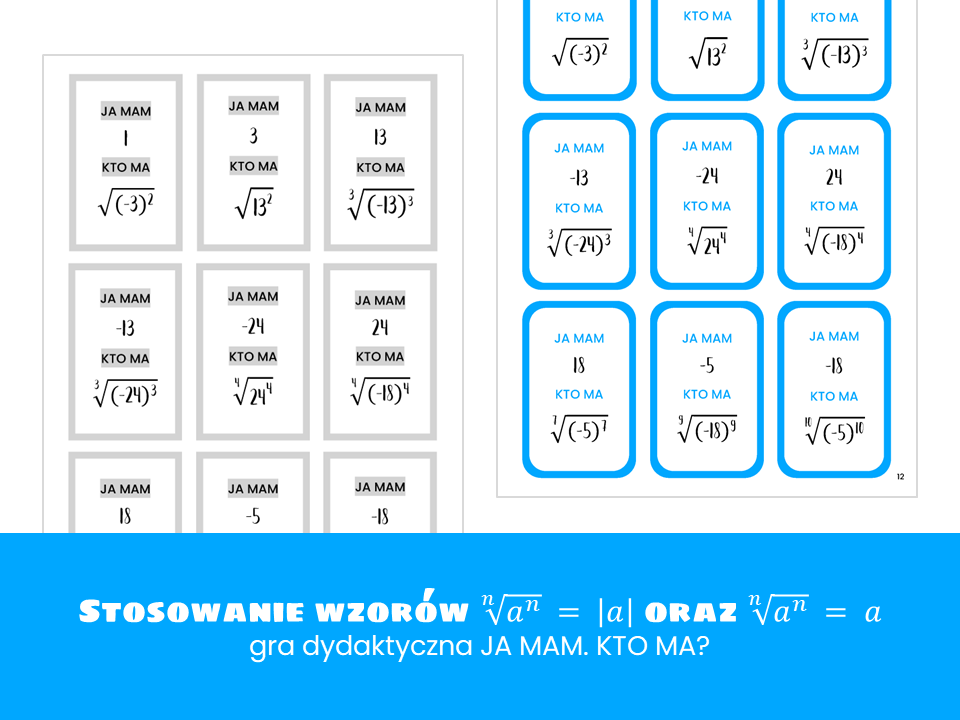
Matematyka. Pierwiastek z potęgi. Gra dydaktyczna. Ja mam. Kto ma
Ocena. Kalkulatory online wykonują obliczenia potęg i pierwiastków. Na stronach można również znaleźć wykresy i wzory na potęgi i pierwiastki. Nasza strona internetowa umożliwia łatwe i szybkie obliczanie. 440 Share 107K views 10 years ago Pierwiastkowanie, pierwiastki, działania na pierwiastkach https://matfiz24.pl/pierwiastki/pierw. Pierwiastek z pierwiastka obliczamy pierwiastkując najpierw. Kurs: Algebra 2 > Rozdział 6. Lekcja 1: Wykładniki wymierne. Wstęp do potęg wymiernych. Potęga jako pierwiastek. Zapisywanie pierwiastków jako potęg o wykładniku wymiernym. Potęgi ułamkowe. Trudniejsze zadania z ułamkowym wykładnikiem potęgi. Równanie wykładnicze, w którym wykładniki sa liczbami wymiernymi. Matematyka >. 1. Jeżeli jest liczbą całkowitą nieparzystą, liczba ma dokładnie jeden pierwiastek -tego stopnia.
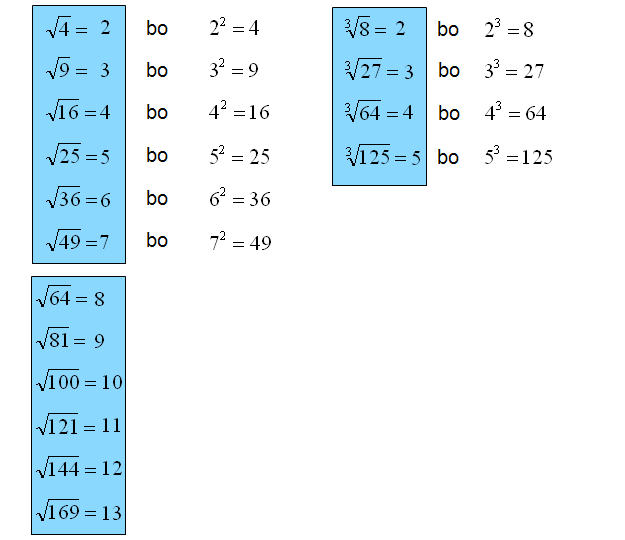
Pierwiastkowanie MatFiz24.pl
★☆★ JAK ZROZUMIEĆ PIERWIASTKI I POTĘGI ★☆★Czyli wszystko co musisz wiedzieć o pierwiastkach i potęgach.Jeśli chcesz wesprzeć to co robię, to możesz:☕️ Ufundo. Zamiana pierwiastka na potęgę - YouTube Kurs matematyki dla liceum.Kanał prowadzony przez Fundację "Pasja Nauki", zapraszamy też na korepetycje i kursy maturalne: www.pasjanauki.plfb:.
Pierwiastek n-tego stopnia z liczby a równa się b, gdy b do potęgi n-tej jest równe a Pierwiastkowanie jest to działanie matematyczne, które jest odwrotnością względem potęgowania. Pierwiastki to nic innego jak odwrotności potęg. https://matfiz24.pl/pierwiastki/pierwiastek-z-potegiFilm przedstawia działanie matematyczne: "pierwiastkowanie kwadratu". Należy pamiętać, że podczas pierwia.

prosze o pomoc wzory skroconego mnozenia (5 pierwiastek 11 +3
Potęgi Dla liczby rzeczywistej i naturalnej : ( razy) - dla - dla - dla - dla parzystego - dla nieparzystego Pierwiastki dla = dla i dla i Usuwanie niewymierności z mianownika Narzędzia Obliczanie potęgi Obliczanie pierwiastka Wzory dla potęg i pierwiastków. Pierwiastek arytmetyczny. Pierwiastkiem arytmetycznym a n stopnia n z liczby a ≥ 0 nazywamy liczbę b ≥ 0 taką, że b n = a. W szczególności, dla dowolnej liczby a zachodzi równość: a n = | a |