Pola i obwody figur płaskich Obwód i pole powierzchni są pojęciami, których często używamy w życiu codziennym. Obwód wielokąta to suma długości jego wszystkich boków. żadnego wzoru, wystarczy zmierzyć jego wszystkie boki, a następnie otrzymane długości dodać. 1. Czym jest pole i obwód figury? 2. Wzory na pola i obwody figur płaskich 2.1. Wzór na pole i obwód kwadratu 2.2. Wzór na pole i obwód trójkąta 2.3. Wzór na pole i obwód prostokąta 2.4. Wzór na pole i obwód trapezu 2.5. Wzór na pole i obwód rombu 2.6. Wzór na pole i obwód równoległoboku 1. Czym jest pole i obwód figury?
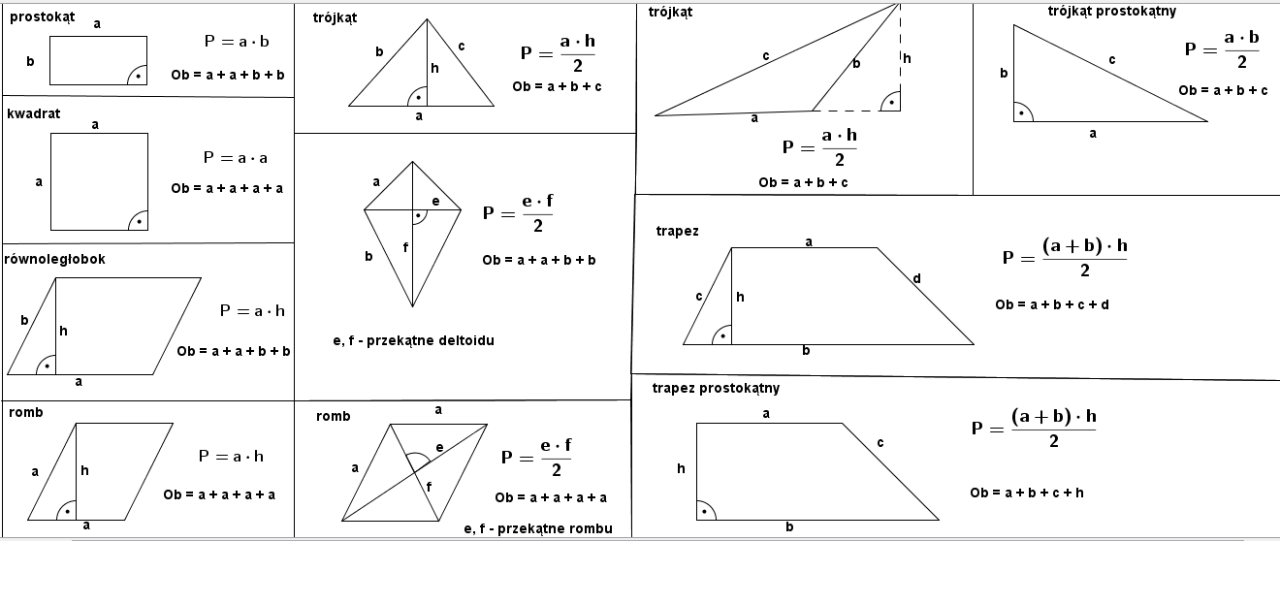
Wzory i rysunki GeoGebra
Pola figur płaskich mają jednostki kwadratowe (np. ) - omówione w następnym podrozdziale. Zanim przedstawimy poszczególne wzory, należy jeszcze wyjaśnić dwa pojęcia: wysokość figury - jest to odcinek łączący jeden z wierzchołków figury i przeciwległy bok (podstawę), opuszczony na ten bok pod kątem prostym. Oznaczamy literą „h". Przykład: Pola i obwody figur płaskich Pole i obwód koła Pole koła Po = π R2 Obwód okręgu (koła) L = 2 π R R - promień okręgu Pole trójkąta P∆ = ½ Podstawa ∙ wysokość Patrz także Wzór Herona Obwód trójkąta O = a + b + c a, b, c - długości boków trójkąta Pole prostokąta Pprostokąta = a ∙ b Obwód prostokąta Oprostokata = 2 ( a + b) Pole kwadratu Dla klasy 1 gimnazjum Learn with flashcards, games, and more — for free. Pola i obwody figur płaskich Materiał nie spełnia wymogów WCAG, natomiast może być wykorzystywany jako materiał dydaktyczny. W prezentacji uczeń znajduje pytania i odpowiedzi związane z polami i obwodami typowych figur ( wzory ), przykładowo rozwiązane zadania - uczeń śledzi ich rozwiązywanie na monitorze

obwody figur płaskich School Study Tips, School Help, Math Work, Fun
Pola i obwody figur płaskich W prezentacji uczeń znajduje pytania i odpowiedzi związane z polami i obwodami typowych figur ( wzory ), przykładowo rozwiązane zadania - uczeń śledzi ich rozwiązywanie na monitorze. Są też zadania do samodzielnego wykonania. Pobierz załącznik Plik PPS o rozmiarze 1.42 MB w języku polskim Opinie - Pola i obwody figur płaskich. 1×2 = DODAJ. Może Ci się przydać: Pole powierzchni równoległoboku - wzór ; Zobacz również. pola figur płaskich 07.Dziękuję 06. Podsumowanie 05. Pole trapezu 04. Pole trójkąta 03. Pole równoległoboku i rombu 02. Pole prostokąta i kwadratu Mathematics Primary School 1.25K subscribers Subscribe 3.7K views 5 years ago Poradniki Matematyczne See how to calculate the circuits of flat figures in mathematics. It is very easy. If you liked.
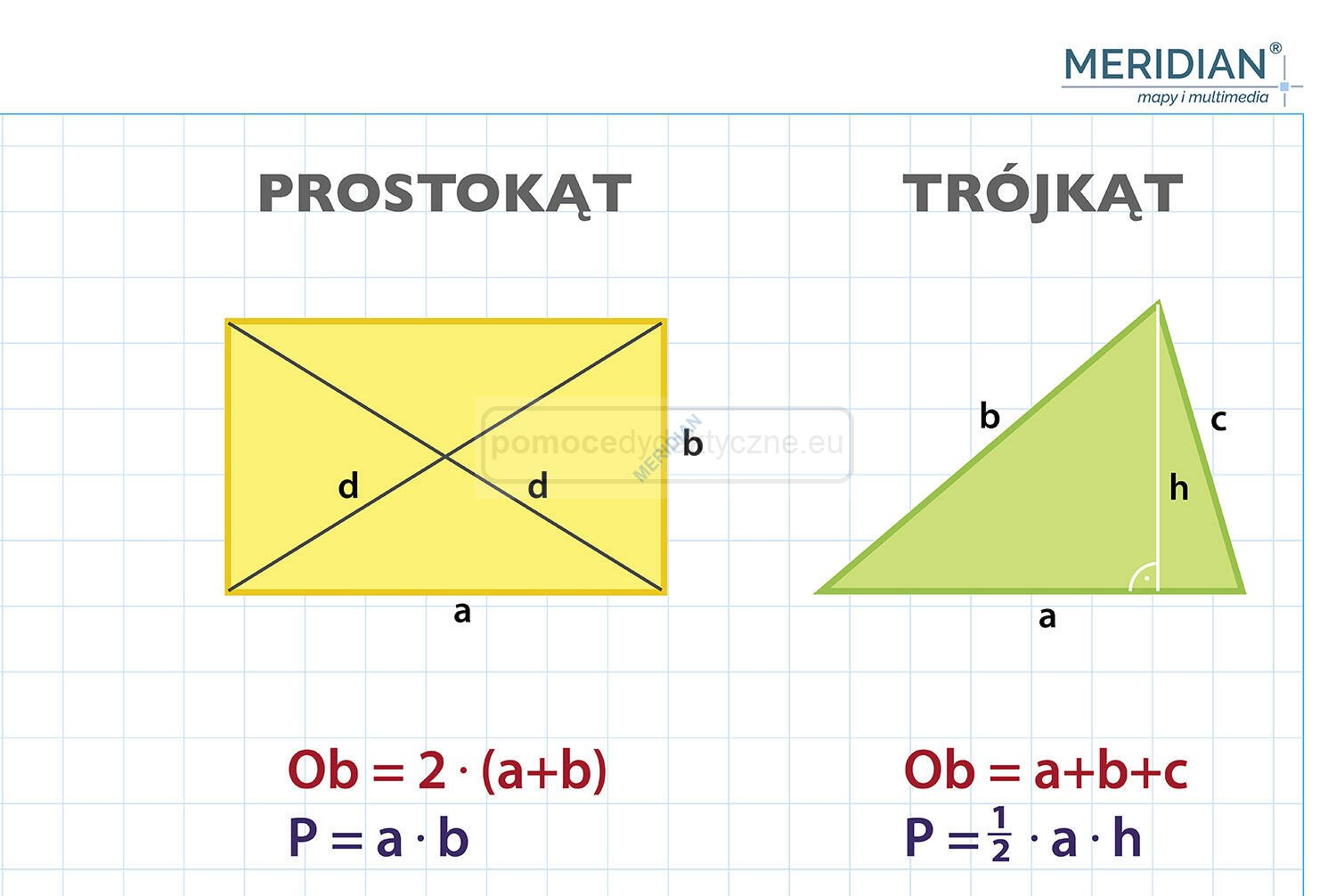
Pola i obwody figur płaskich ścienna plansza dydaktyczna
POLA I OBWODY FIGUR PŁASKICH Ostrosłup Walec 2 P = π r = 2 π rh b = 2 P + c p P b 2 P = 2 π r + 2 π rh P - pole podstawy p - pole powierzchni bocznej Stożek 2 P = π p r = π rl = P + P c p b = π c 2 r + π rl - pole podstawy p - pole powierzchni bocznej b Siatka stożka P = π p 2 r α 2 P = π l o 360 = P ⋅ p h 2 V = π r h Pola i obwody figur płaskich Plakat ☆ ☆ ☆ ☆ ☆ Plakat dydaktyczny przedstawiający definicje podstawowych figur geometrycznych ze wzorami na obliczenie pola. Format B2 (pionowo) - 48x68 cm 18,90 zł Dodaj do koszyka Dostępne również w pakietach promocyjnych Dostawa do 5 dni roboczych Przesyłka w tubie Darmowa dostawa
Pole stożka: P = Ppostawy + Ppowierzchni bocznej. P = π R2 + π R l. h - wysokość, r - promień podstawy. l - tworząca stożka. Poniższych wzorów nie trzeba uczyć się na pamięć. Wystarczy, że zrozumiemy, jak zostały stworzone i możemy uzyskać je sami (czasami sprawia to pewną trudność uczniom gimnazjum, dlatego podamy wzory dla wszystkich istotnych figur). Obwód figury płaskiej jest sumą wszystkich jej boków. Oblicz obwód prostokąta o długości 6cm i.

Pola i obwody figur płaskich ARAN
Zastosowanie wzorów na pola figur (na poziomie ucznia klasy 5) Podstawowa. Podstawowa. Podstawowa. Pole wielokąta (na poziomie ucznia klasy 5) Podstawowa. Matematyka. Geometria. Podstawowa. OBWODY FIGUR PŁASKICH. 𝑷= ∙ 𝒍= 𝜶 ° ∙ 𝝅𝒓 długość łuku. 3 POLA I OBJĘTOŚCI FIGUR PRZESTRZENNYCH GRANIASTOSŁUP - pole powierzchni całkowitej i pole powierzchni bocznej = + = ∙ - objętośd graniastosłupa = ∙ - pole podstawy, - obwód podstawy,




