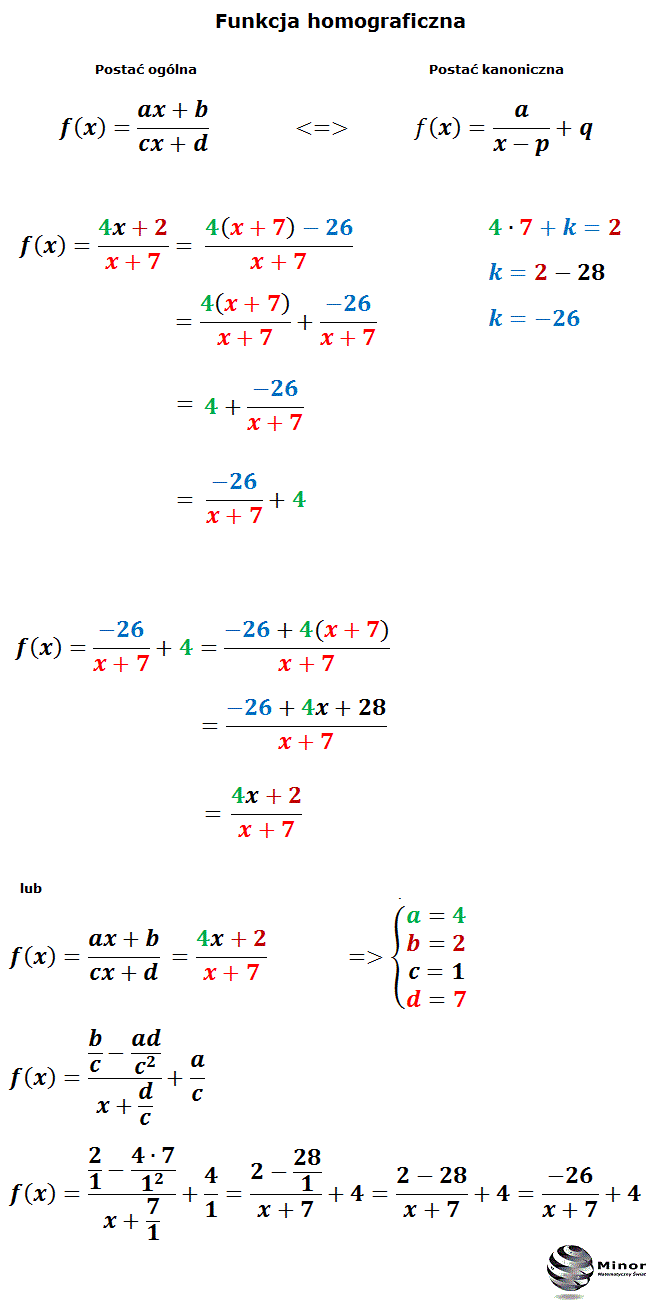Postać kanoniczna funkcji homograficznej . Liceum ogólnokształcące i technikum. Kategorie. Matematyka. Słowa kluczowe. hiperbola funkcje funkcja homograficzna funkcja wymierna postać kanoniczna funkcji homograficznej. Udostępnij Wprowadzenie. Przeczytaj. Symulacja interaktywna. Funkcja homograficzna. Wykres przykładowej funkcji homograficznej: y = 1/x. Dla każdego niezerowego x liczba y przedstawia jego odwrotność. Funkcja homograficzna, homografia [1] - różnie definiowany typ funkcji wymiernej : w sensie szerokim jest to każdy iloraz funkcji liniowych niebędący stałą:

Blog matematyczny Minor Matematyka Funkcja homograficzna
Funkcja homograficzna jest monotoniczna na każdym z przedziałów oraz . Funkcja jest: przedziałami malejąca, gdy oraz. przedziałami rosnąca, gdy . Wykres funkcji homograficznej , gdzie oraz powstaje w wyniku przesunięcia równoległego wykresu pewnej hiperboli o pewien wektor. Zauważmy w tym celu, że dla wszystkich mamy. Zaznacz prawidłową odpowiedź. Postać kanoniczna funkcji homograficznej f(x)= (2x+4)/(x-3)Te zadanie pochodzi ze strony https://zpe.gov.pl/a/symulacja-interak. Dziedziną funkcji homograficznej jest zbiór R- {}. Przykład 1. Która funkcja jest funkcją homograficzną ? Wybierz tą funkcję i narysuj jej wykres: f(x)= g(x)= h(x)= Rozwiązanie: Funkcja f nie jest homograficzna, bo c=0, g także ponieważ ad-cb = 12-12=0. Jedyną funkcją homograficzną jest funkcja h (przykład c) ). Postać kanoniczna funkcji homograficznej. Autor: zs1lubin - R. Kędzia. Nowe zasoby. Reguła Eulera; Co to za czworokąt? Boże Narodzenie - do druku 3D; Obrót sześciokąta wokół osi OZ; Odcinki równoległe na siatce; Odkryj zasoby. Wielościan/Solid J08; Wykres funkcji homograficznej;
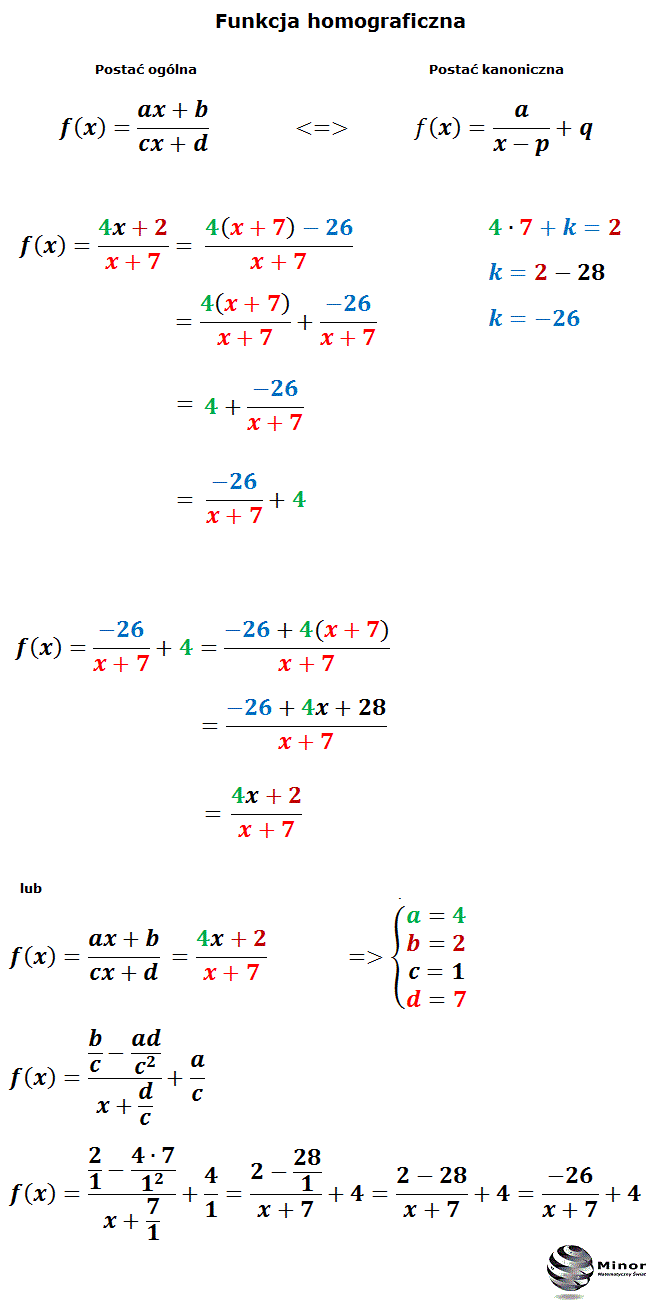
Blog matematyczny Minor Matematyka Funkcja homograficzna
Funkcja homograficzna postać kanoniczna. 7 przykładów.0:00 wstęp0:16 1 przykład3:02 2 przykład5:00 3 przykład7:07 4 przykład9:21 5 przykład10:25 6 przykład11. Postać kanoniczna funkcji to . Przykład 2 Na podstawie wykresu funkcji podamy własności funkcji, które można określić na podstawie postaci kanonicznej funkcji homograficznej. Rozwiązanie Aby narysować wykres funkcji należy wykres funkcji przesunąć o wektor . Własności funkcji:;" 4 Ã 4Ã Ã 4Ã " 4 Skoro asymptoty wykresu funkcji przecinają się w punkcie -4,-2, to każda funkcja postaci: f x = r x + 4-2, r ≠ 0, określa postać kanoniczną tej funkcji. Przykład 5 Wyznaczymy wzór funkcji homograficznej wiedząc, że jest ona rosnąca w każdym z przedziałów: - ∞ , - 3 , - 3 , ∞ , Z W f = ℝ ∖ 4 oraz do wykresu funkcji należy punkt - 1 , 3 . Funkcja homograficzna - wykres i własności, postać ogólna i kanoniczna Funkcje. Odsłon: 1118 . Funkcja homograficzna. wykres i własności. postać ogólna i kanoniczna . Wpisz wzór funkcji w pola w dolnej części.. Funkcja kwadratowa - największa i najmniejsza wartość funkcji kwadratowej w przedziale domkniętym Poprzedni artyku.

Postać kanoniczna funkcji homograficznej YouTube
Telewizja internetowa MatematykaTV Damian Wziętek matematyka, funkcja wymierna. Funkcja homograficzna, homografia - różnie definiowany typ funkcji wymiernej: w sensie szerokim jest to każdy iloraz funkcji liniowych niebędący stałą: . Wykres przykładowej funkcji homograficznej: y = 1/x. Dla każdego niezerowego x liczba y przedstawia jego odwrotność. Powyższy wzór jest znany jako postać ogólna homografii, a.
Funkcja homograficzna. Funkcję wymierną postaci f(x) = ax+b cx+d, gdzie ad ≠ bc, i c ≠ 0 nazywamy funkcją homograficzną. Jeżeli a ≠ 0 to miejscem zerowym funkcji homograficznej jest punkt x = − b a . Funkcja f(x) = ax+b cx+d dla c ≠ 0 i ad - bc > 0 jest rosnąca w swojej dziedzinie, dla c ≠ 0 i ad - bc < 0 jest malejąca w. Warunek zapewnia, że nie zredukuje się do funkcji stałej, natomiast warunek gwarantuje, że nie będzie liniowa. Własności funkji homograficznej. Dziedziną jest zbiór liczb rzeczywistych z wyłączeniem miejsca zerowego mianownika, tj. . Zbiorem wartości jest zbiór liczb rzeczywistych oprócz , zatem .

Postać kanoniczna funkcji homograficznej GeoGebra
Dziedziną funkcji homograficznej jest zbiór ℝ ∖-d c. Powyższy wzór to postać ogólna funkcji homograficznej. Postać kanoniczna funkcji homograficznej. f x = r x-p + q, r ≠ 0, D f = ℝ ∖ p. Wykresem każdej funkcji homograficznej jest hiperbola. Wykres funkcji f x = r x-p + q powstaje w wyniku przesunięcia wykresu funkcji g x = r. Szczególnym przypadkiem funkcji homograficznej jest funkcja b/x (często oznaczana po prostu a/x, wtedy formalny parametr b jest przemianowany na a): y = b x y=\frac{b}{x} y = x b Funkcja b/x nie posiada miejsc zerowych , a jej punktem symetrii jest początek układu współrzędnych (punkt (0,0)) .