Promień (oznaczany literą r od łac. radius) - odcinek łączący środek koła, okręgu, kuli lub sfery z dowolnym punktem położonym na jej brzegu, a także długość tego odcinka. Długość promienia jest w tym przypadku zawsze równa połowie długości średnicy, co wyraża wzór Promień okręgu (koła) jest to odcinek łączący środek okręgu z dowolnym jego punktem. Pole i obwód koła - wzory Pole koła o promieniu r r wynosi P = πr2 P = π r 2. Obwód koła o promieniu r r wynosi L = 2πr L = 2 π r. Przykład 1: Cięciwa okręgu ma długość 8 cm i jest oddalona od jego środka o 3 cm. Promień tego okręgu ma długość: a) 3 cm b) 4 cm

oblicz promień okręgu wpisowego o trójkąt prostokątny jeśli jego
Na szczęście nasz kalkulator potrafi obliczyć promień okręgu w każdej z tych sytuacji. Co więcej, nie musisz decydować, który wzór na promień jest potrzebny: po prostu wprowadź którąś wartość do odpowiedniego pola kalkulatora, a on automatycznie zastosuje odpowiedni wzór i wyliczy wszystkie niewiadome. Okrąg, to zbiór tylko tych punktów, które są położone na brzegu koła. Pojęcia cięciwy, średnicy oraz stycznej dotyczą również koła, ponieważ okrąg jest brzegiem koła. Środek koła oczywiście należy do koła. Obwód koła (czyli długość okręgu) możemy obliczyć ze wzoru: Ob = 2πr. gdzie r - to promień koła. Pole. Pojęcie okręgu może być uogólnione na dowolną przestrzeń metryczną w naturalny sposób. Odległością wg której definiuje się okrąg jest ustalona metryka. Tak więc, w dowolnej przestrzeni metrycznej okrąg ze środkiem i promieniem to zbiór punktów. W tym rozumieniu często zamiast słowa „okrąg" stosuje się słowo „sfera". Promień okręgu Ta odległość nazywa się promień okręgu. ń Promień. Promie Który z odcinków na okręgu przedstawionym poniżej jest promieniem? Zaznacz wszystkie odpowiedzi, które pasują: A A A B B B C C C A B C

Przyprostokątne trójkąta prostokątnego mają długości 6 i 8. Oblicz
Zadanie 1 Oblicz promień jeśli wiesz, że średnica ma 56 cm . Wynik podaj w metrach. Rysunek pomocniczy : Dane : Średnica ( d ) - 56 cm Promień ( r ) - x wzór na promień - r = 21 * d Rozwiązanie : r = 21 * d r = 21 * 56 r = 256 r = 28 cm Pamiętaj ! 1 m = 100 cm 28 cm = 0,28 m ( przesuwamy przecinek o dwa miejsca w lewą stronę) Kurs: Geometria (cały materiał) > Rozdział 4. Lekcja 5: Dwusieczne kąta. Odległość pomiędzy punktem a prostą. Okrąg wpisany w trójkąt i jego środek. Promień okręgu wpisanego, pole i obwód. Matematyka >. Geometria (cały materiał) >. Własności trójkątów >. Dwusieczne kąta. Możemy pomnożyć obie strony przez średnicę i wyjdzie nam obwód = Π * średnica Albo, ponieważ średnica to 2 * promień możemy napisać, że obwód = Π * 2 * promień Ten wzór najczęściej zapisuje się w taki sposób: 2Πr Spróbujmy zastosować go w praktyce. Powiedzmy, że mamy koło. Takie koło. Promień okręgu to odcinek pomiędzy jego środkiem z dowolnym punktem na okręgu. W jednym okręgu mamy nieskończenie wiele promieni, rozchodzących się we wszystkich kierunkach od środka S. Każdy promień ma dokładnie tę samą długość.

Trójkącie prostokątnym cosinus jednego z kątów jest równy 12/13 a
Promień okręgu wskazuje współczynnik r. Uważajmy jednak, bo wartość po prawej stronie równania okręgu, to nie promień sam w sobie, ale promień podniesiony do kwadratu. W podanym przykładzie: Po prawej stronie znajduje się wartość 9, co oznacza, że promień do kwadratu wynosi 9. Aby uzyskać promień, należy więc tę wartość. Wyznacz współrzędne środka okręgu i jego promień. Równanie okręgu. Okrąg w układzie współrzędnych.Tłumacząc zadania wychodzę z założenia, że potrafisz dodawa.
3000 km Wydrukuj mapę Pobierz mapę Narysuj promień wokół lokalizacji na mapie. Umieść okrąg o promieniu wokół lokalizacji w Mapach Google, aby pokazać odległość od tego punktu we wszystkich kierunkach. Zadanie 1. Dany jest okrąg o równaniu (x + 3)2 + (y − 4)2 = 25 . Środkiem S tego okręgu jest punkt: A. S = (−3, −4) B. S = (3, 4) C. S = (3, −4) D. S = (−3, 4) Film Youtube Odp Zadanie 2. Odległość między środkami okręgów o równaniach (x + 1)2 + (y − 2)2 = 9 oraz x2 +y2 = 10 jest równa A. 5-√ B. 10−−√ − 3 C. 3 D. 5 Film Youtube Odp Zadanie 3.
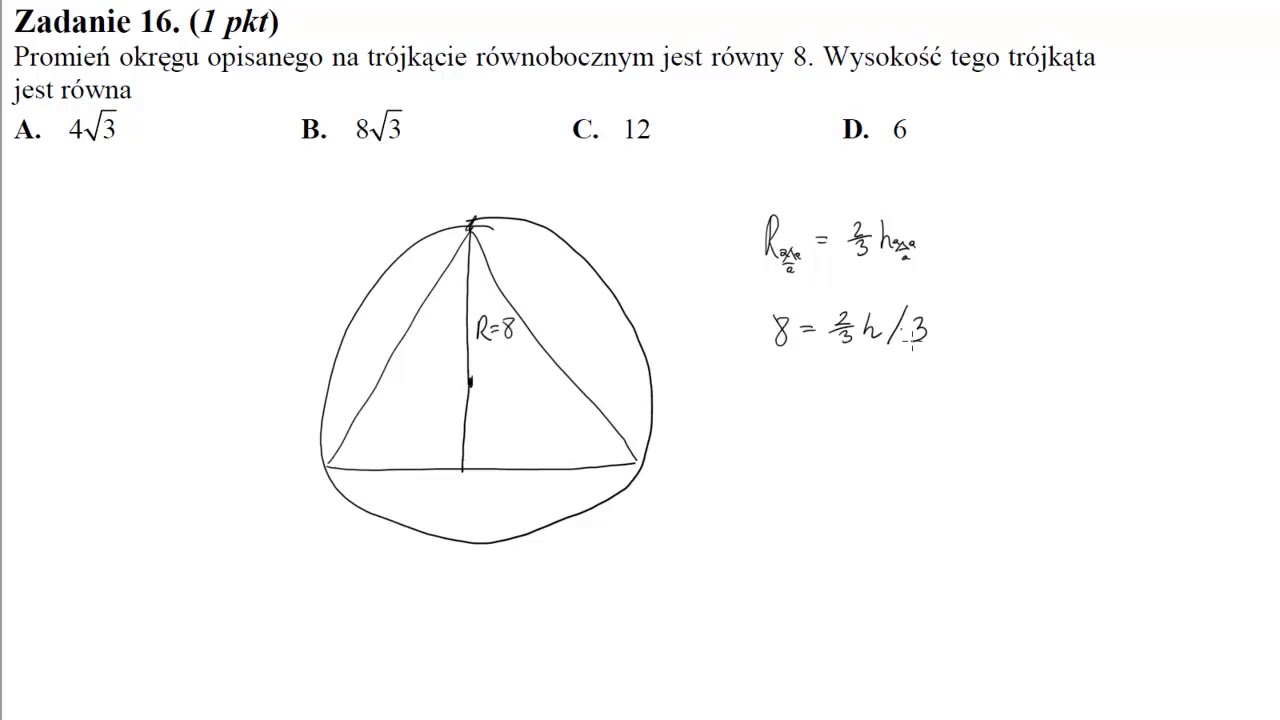
16 Promień okręgu opisanego na trójkącie równobocznym jest równy 8
Aby policzyć promień okręgu opisanego na trójkącie biorę długość dowolnego boku trójkąta i dzielę przez podwojony sinus kąta znajdującego się naprzeciwko tego boku. Trójkąt oparty na średnicy jest prostokątny. Środek okręgu opisanego na trójkącie znajdujemy rysując symetralne boków trójkąta. Wzór na promień okręgu wpisanego w trójkąt. Środek okręgu wpisanego w trójkąt znajdujemy rysując dwusieczne kątów trójkąta.