praktyce stosuje się częściej zapis ułamkowy; · d = b · c. | = 5,4 − 3,6 = 1,8. 3,6 = 1,8. 1,2. to . ∙ 1,8 = 1,2 ∙ 3,6. 1,8 = 4,32|: 1,8. = 2,4. Ćwiczenie 4. Wyznacz , Podział odcinka na 3 równe części: https://www.youtube.com/watch?v=iYqGHNEUctg. https://spodnietalesa.wordpress.com/grupa-iv/podzial-odcinka-na-rowne-czesci/ Ćwiczenie 5. Twierdzenie Talesa mówi, że jeżeli przetniemy kąt prostymi równoległymi, to stosunki odpowiednich otrzymanych odcinków będą równe. Na powyższym rysunku kąt α przecięto prostymi równoległymi k i l. Wówczas zgodnie z twierdzeniem Talesa zachodzą następujące proporcje: |AB| |AC| = |BD| |CE| = |AD| |AE|. z których wynika również, że:
Twierdzenie Talesa MatFiz24.pl YouTube
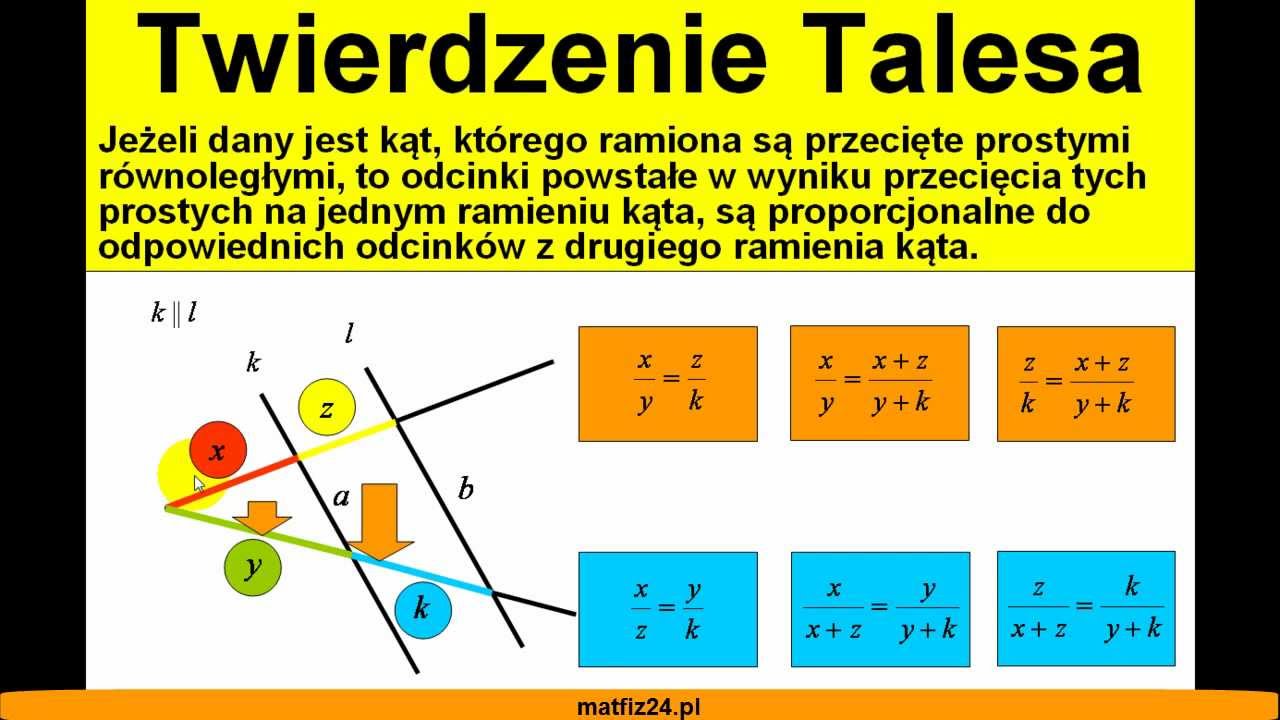
Metoda i forma pracy. Metoda problemowo - analityczna, pokaz. Formy pracy: praca z całą klasą, praca w grupach czteroosobowych. 3. Środki dydaktyczne. kartki z treścią zadań - „W kręgu twierdzenia Talesa" , schemat - „Plan rozwiązywania zadań", pokaz programu PowerPoint XP „Zastosowanie twierdzenie Talesa", foliogram + grafoskop. 4. Twierdzenie Talesa. 1 klasa liceum na podbudowie szkoły podstawowej. Na ostatniej lekcji nauczyliśmy się: podawać definicję trójkątów przystających oraz cechy przystawania trójkątów, wskazywać trójkąty przystające, stosować nierówność trójkąta do rozwiązywania zadań. Twierdzenie Talesa. Jeżeli ramiona kąta przetniemy kilkoma prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta. Wygodnie jest długości odcinków oznaczyć małymi literami. Powyższe zadanie można wytłumaczyć na wiele sposobów: Metoda spadających odcinków - Twierdzenie Talesa informuje nas, że proporcje możemy budować opuszczając odcinki z jednego ramienia kąta na odcinki z drugiego ramienia kąta. Strzałki pokazują kierunek spadania odcinków w Twierdzeniu Talesa.

Twierdzenie Talesa
Twierdzenie Talesa możemy też rozbudować o sytuacje, w której dwie proste równoległe przechodzą przez dwie proste przecinające się: Bazując na oznaczeniach, moglibyśmy zapisać, że: a b = d c a b = d c. Sprawdźmy teraz wykorzystanie twierdzenia Talesa w praktyce. Przykład 1. Oblicz długość odcinka x x, wiedząc że proste k k oraz l l są równoległe. Na ekranie prezentuję tw. Talesa i twierdzenia wynikające z niego, wyświetlam zadania na zastosowanie poznanych twierdzeń. Uczniowie przy tablicy rozwiązują zadania. Otrzymują oceny. Utrwalenie umiejętności - praca w grupach. Klasę dzielę losowo na grupy. Grupy otrzymują karty z czterema zadaniami do rozwiązania. Na wykonanie pracy. Korzystając z Twierdzenia Talesa wiemy, że prawdziwe jest następujące równanie: Obliczamy długość : Przykład: W trójkącie równoramiennym poprowadzono odcinek równoległy do boku w taki sposób, że punkty oraz podzieliły ramiona tego trójkąta w stosunku (licząc od wierzchołka ). Zadanie 1. Podaj założenia i tezę twierdzenia Talesa. Jaką postać ma to twierdzenie? Przepro-wadź następującą konstrukcję pomocniczą i prześledź dowód twierdzenia Talesa przedstawiony przez Euklidesa. Konstrukcja pomocnicza: Narysować dowolny kąt płaski AOB. Poprowadzić dwie proste równoległe przecinające ramiona OA.

Twierdzenie Talesa YouTube
Twierdzenie 1. Prosta równoległa do jednego boku trójkąta i przecinająca pozostałe boki tego trójkąta odcina z tego trójkąta trójkąt o bokach proporcjonalnych do boków danego trójkąta. A D A B = A E A C = D E B C. Twierdzenie 2. W trójkącie dwusieczna kąta wewnętrznego dzieli bok przeciwległy na odcinki proporcjonalne do boków przyległych. KARTA PRACY. Zad. 1. Skonstruuj obraz trójkąta o bokach 1, 3, 3 w jednokładności o skali k = 2.
Twierdzenie Talesa - ćwiczenia. Wykonaj poniższe ćwiczenia aby utrwalić materiał z tego artykułu. Każde ćwiczenie możesz wykonać samodzielnie i sprawdzić, czy prawidłowo zostało wykonane. W każdej chwili możesz też zobaczyć prawidłową odpowiedź do danego zadania. Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego) RóŽne proste A C' i BD przecinaja sie w punkcie P, przy czym spelniony jest jeden z warunków: punkt A leŽy wewnatrz odcinka PC oraz punkt B leŽy wewnatrz odcinka PD lub punktA leŽy na zewnatrz odcinka PC oraz punkt B leŽy na zewnqtrz odcinka PD.

Twierdzenie Talesa wraz z twierdzeniem odwrotnym do niego • Złoty
KARTY PRACY UCZNIA. Twierdzenie Pitagorasa i jego zastosowanie. opracowanie: mgr Teresa Kargol, nauczyciel matematyki. w PSP nr 162 w Łodzi. Karty pracy to materiały pomocnicze, które mog słu y do. ż ć. samodzielnej pracy ucznia. Zawarte w nich tre ści s ą uło żone w taki sposób, Twierdzenie Talesa brzmi następująco: Jeżeli ramiona kąta AOA′ są przecięte dwiema prostymi równoległymi AA′ i BB′, to długości odcinków wyznaczonych przez te proste na jednym ramieniu tego kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na jego drugim ramieniu:




