Twierdzenie odwrotne do twierdzenia Talesa. Twierdzenie odwrotne do twierdzenia Talesa brzmi następująco: Jeżeli odcinki wyznaczone przez dwie proste na jednym ramieniu kąta (oznaczonym na rysunku jako 1) są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta (oznaczonym na rysunku jako 2), to. Twierdzenie Talesa mówi, że jeżeli przetniemy kąt prostymi równoległymi, to stosunki odpowiednich otrzymanych odcinków będą równe. Na powyższym rysunku kąt α przecięto prostymi równoległymi k i l. Wówczas zgodnie z twierdzeniem Talesa zachodzą następujące proporcje: |AB| |AC| = |BD| |CE| = |AD| |AE|. z których wynika.
Blog matematyczny Minor Matematyka Twierdzenie Talesa i odwrotne
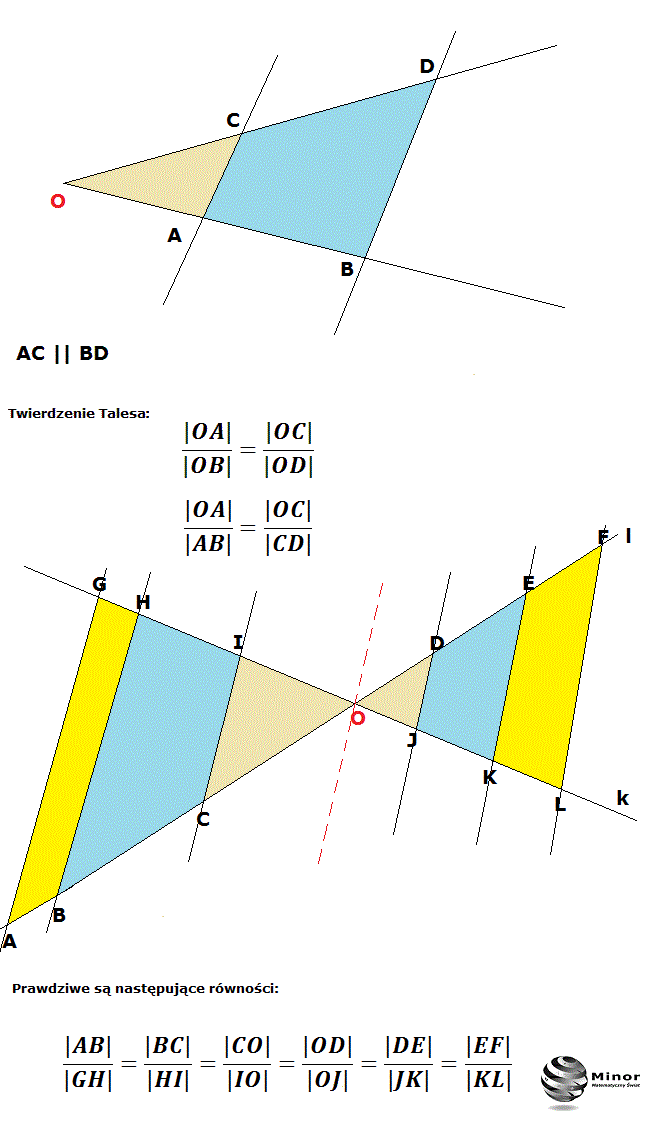
Twierdzenie Talesa: Jeżeli ramiona kąta są przecięte dwiema prostymi równoległymi, to stosunek odcinków (mierzonych od wierzchołka kąta O) wyznaczonych przez te proste k i l na jednym ramieniu kąta jest równy stosunkowi odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu tego kąta. Twierdzenie Talesa - wzór Twierdzenie Talesa głosi, że jeśli dany kąt zostanie przecięty przez dwie proste równoległe, to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta są proporcjonalne do odcinków wyznaczonych na drugim ramieniu. Twierdzenie Talesa - jedno z podstawowych twierdzeń geometrii euklidesowej, tradycja przypisuje jego sformułowanie Talesowi z Miletu. Jest też ważnym twierdzeniem geometrii afinicznej. Link do zbioru zadań:http://www.matemaks.pl/matura-rozszerzona-kurs-czesc-32-zadania.htmlLink do całego kursu:http://www.matemaks.pl/matematyka-matura-rozsze.
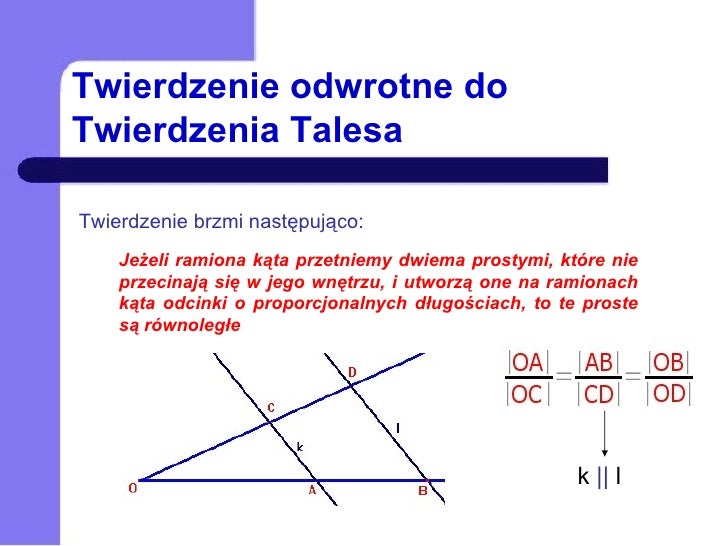
Twierdzenie odwrotne do Twierdzenia Talesa
Kurs maturalny z matematyki - zakres podstawowy:http://www.matspot.pl/matura/matura_kurs.htmlzobacz też:http://www.matspot.pl/https://www.facebook.com/mathspot/ Twierdzenie Talesa najczęściej spotyka się w dwóch przypadkach: Przypadek 1: Ze względu na często popełniane błędy zwróćmy uwagę na to, że dla poniższego zachodzi nierówność: a c ≠ b d a c ≠ b d. Wiele osób popełnia błąd zakładając, że powyższa nierówność jest równością. Film, w którym omawiane jest Twierdzenie Talesa i Twierdzenie odwrotne do twierdzenia Talesa. Wiedza ta jest potrzebna w dziale Planimetria w Liceum Ogólnokształcącym. Film jest ściśle. Twierdzenie Talesa. Jeżeli ramiona kąta przetniemy dwiema prostymi równoległymi, to długości odcinków wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta.. Twierdzenie odwrotne do twierdzenia Talesa. Jeśli odcinki wyznaczone.
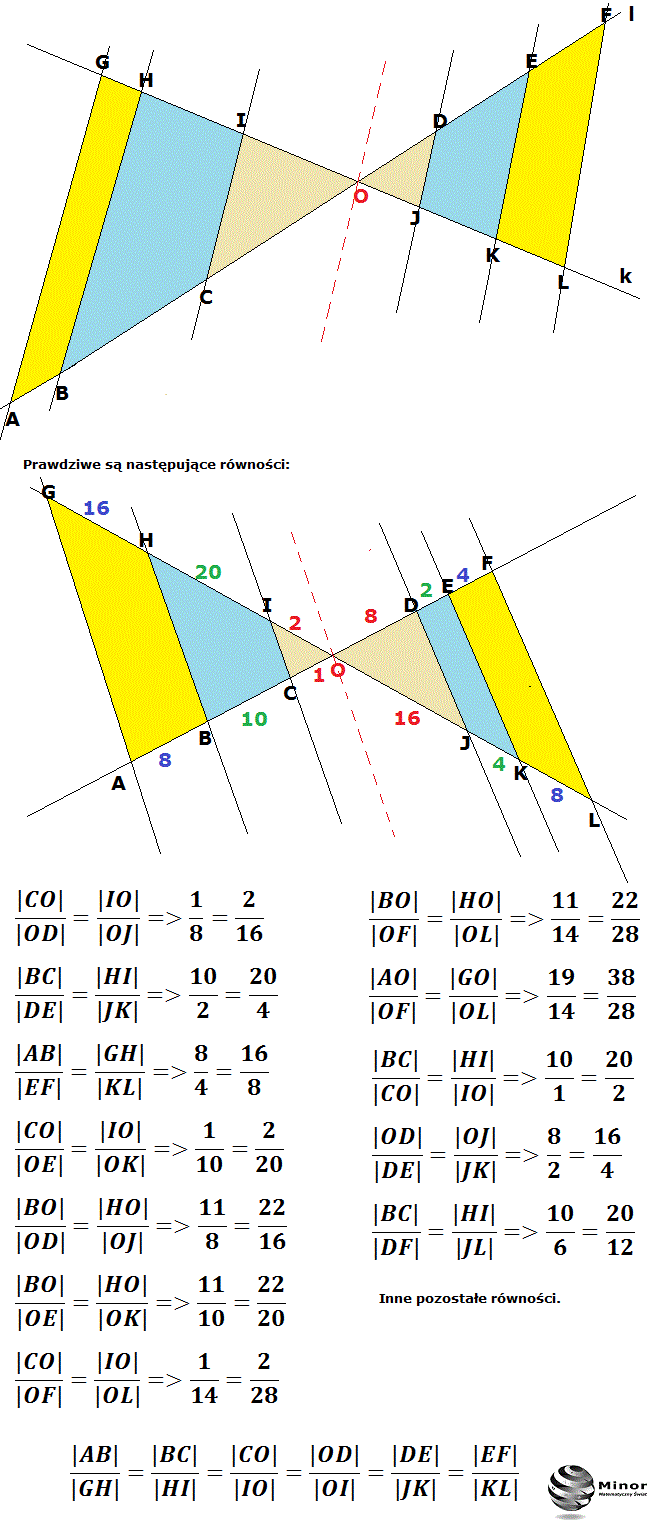
Blog matematyczny Minor Matematyka Twierdzenie Talesa i odwrotne
Twierdzenie odwrotne do twierdzenia Talesa. Liceum ogólnokształcące i technikum. Matematyka. kąt planimetria linia środkowa w trapezie twierdzenie odwrotne do twierdzenia Talesa. Udostępnij. WprowadzeniePrzeczytajGaleria zdjęć interaktywnychSprawdź sięDla nauczycielawork. Twierdzenie tutaj prezentowane sformułował prawdopodobnie Tales z Miletu, który żył w latach około 620-540 p.n.e. Tales był greckim filozofem, astronomem i matematykiem, twórcą jońskiej filozofii przyrody, w której woda była uważana za prapierwiastek rzeczywistości.
Twierdzenie Talesa. Sąsiednie zadania. Zadanie 3166 Zadanie 3167. Zadanie 3168 (tu jesteś) Zadanie 3169 Zadanie 3170. W tym filmie wyjaśniam twierdzenie Talesa i pokazuję jak je stosować na przykładach. - rozwiązanie zadania. formułuje twierdzenie odwrotne do twierdzenia Talesa, opisuje własność odcinka łączącego środki ramion w trójkącie, stosuje poznane fakty i twierdzenia do rozwiązywania problemów geometrycznych. Strategie nauczania: konstruktywizm; konektywizm. Metody i techniki nauczania: dyskusja; praca z ekspertem; Formy pracy:
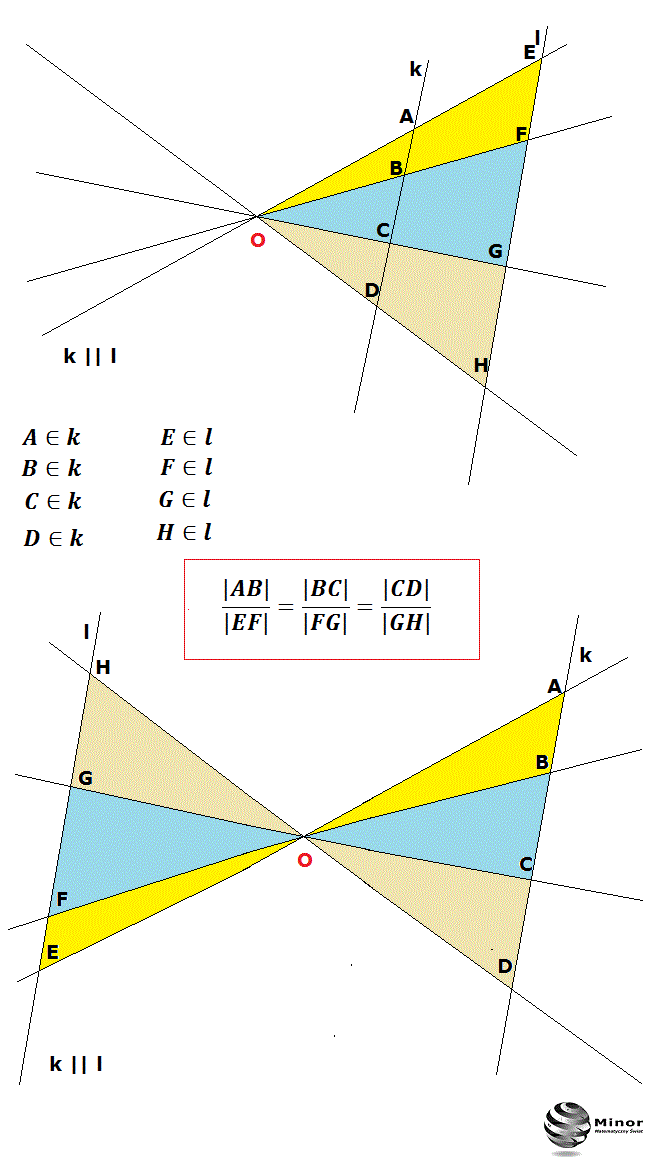
Blog matematyczny Minor Matematyka Twierdzenie Talesa i odwrotne
Twierdzenie odwrotne do twierdzenia Talesa. Źródło: Gordon Johnson, dostępny w internecie: pixabay.com, domena publiczna. Tales z Miletu (VII lub VI w. p. n. e.) jest powszechnie uznawany za pierwszego filozofa i matematyka cywilizacji zachodniej oraz za inicjatora badań nad przyrodą jako nauki. Postrzega się go jako pierwszego filozofa. ZOBACZ aby ZDAĆ MATURĘ w 2023 ️. Dzisiaj w materiale twierdzenie Talesa oraz twierdzenie odwrotne do twierdzenia TalesaChciałbyś bardziej podziękować za moją pracę Poniżej możesz mi.




