Zadanie 1. Dany jest okrąg o równaniu (x + 3)2 + (y − 4)2 = 25 . Środkiem S tego okręgu jest punkt: A. S = (−3, −4) B. S = (3, 4) C. S = (3, −4) D. S = (−3, 4) Film Youtube Odp Zadanie 2. Odległość między środkami okręgów o równaniach (x + 1)2 + (y − 2)2 = 9 oraz x2 +y2 = 10 jest równa A. 5-√ B. 10−−√ − 3 C. 3 D. 5 Film Youtube Odp Zadanie 3. Promień okręgu (koła) jest to odcinek łączący środek okręgu z dowolnym jego punktem. Pole i obwód koła - wzory Pole koła o promieniu r r wynosi P = πr2 P = π r 2. Obwód koła o promieniu r r wynosi L = 2πr L = 2 π r. Przykład 1: Cięciwa okręgu ma długość 8 cm i jest oddalona od jego środka o 3 cm. Promień tego okręgu ma długość: a) 3 cm b) 4 cm
Blog matematyczny Minor Matematyka marca 2014
Podstawowy wzór na obliczenie promienia to : r= 21 * d r - promień d - średnica d = 2 r Jak zastosować wzór na promień w zadaniach ? Zadanie 1 Oblicz promień jeśli wiesz, że średnica ma 56 cm . Wynik podaj w metrach. Rysunek pomocniczy : Dane : Średnica ( d ) - 56 cm Promień ( r ) - x wzór na promień - r = 21 * d Rozwiązanie : r = 21 * d Pole koła możemy obliczyć ze wzoru: gdzie - to promień koła. Przykład 1. Oblicz obwód i pole koła, którego średnica jest równa . Rozwiązanie: Średnica koła składa się z dwóch promieni. Możemy zatem obliczyć promień koła: Teraz liczymy obwód i pole ze wzorów: W okręgu możemy wyróżnić dwa bardzo ważne kąty: Promień okręgu opisanego można obliczyć ze wzoru: R = abc 4rp gdzie: a, b, c - to długości boków trójkąta, r - to długość promienia okręgu wpisanego w trójkąt, p - to połowa obwodu trójkąta, czyli p = a + b + c 2. Zadanie 1. matura 2024 PP Punkt S jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Promień r łączy środek okręgu O z punktem P na jego brzegu. Promień (oznaczany literą r od łac. radius) - odcinek łączący środek koła, okręgu, kuli lub sfery z dowolnym punktem położonym na jej brzegu, a także długość tego odcinka. Długość promienia jest w tym przypadku zawsze równa połowie długości średnicy, co.

1) promień okręgu wpisanego w trójkąt równoboczny o boku 6 cm ma
Znajdźmy obwód poniższego okręgu: 10. Średnica wynosi 10 , więc możemy wstawić d = 10 do wzoru C = π d : C = π d. C = π ⋅ 10. C = 10 π. I już! Możemy pozostawić odpowiedź w tej formie, zawierającą π . A zatem, obwód tego okręgu wynosi 10 π , w tych samych jednostkach, w jakich podana jest średnica d . Wzory na wymiary koła i okręgu 1. Długość okręgu Długość okręgu jest obliczana następującym wzorem: d=2πr gdzie r - promień okręgu, zaś π, to wartość stała wynosząca w przybliżeniu 3,14 2. Obwód koła Obwód koła liczony jest ze wzoru na długość okręgu: d=2πr gdzie r - promień okręgu, zaś π, to wartość stała wynosząca w przybliżeniu 3,14 3. Wykazać, że wyprowadzony wzór na długość promienia okręgu (koła) wpisanego i opisanego jednocześnie w trapezie równoramiennym w szczególnym przypadku zwraca wzór na długość promienia okręgu (koła) wpisanego i opisanego na tym kwadracie wiedząc, że a=b. 180o Wyznaczyć długość promienia okręgu (koła) wpisanego i opisanego. Ucz się za darmo matematyki, sztuki, programowania, ekonomii, fizyki, chemii, biologii, medycyny, finansów, historii i wielu innych. Khan Academy jest organizacją non-profit z misją zapewnienia darmowej edukacji na światowym poziomie dla każdego i wszędzie.

Promien okregu opisanego na trojkacie prostokatnym ktorego
l = d ⋅ π. d− średnica okręgu. Wzór na pole koła o danym promieniu: P = π ⋅r2. Można również spotkać trochę rzadziej wykorzystywane wzory: Wzór na średnicę koła : d = l π. l− obwód koła lub inaczej długość okręgu. π ≈ 3, 14 − stała liczba niewymierna. Istnieją trzy wzory, za pomocą których możemy obliczyć promień. Możemy wybrać jeden z nich na podstawie tego, która wartość jest nam znana: Promień okręgu z powierzchni koła: jeśli znasz powierzchnię koła P, promień wynosi r = √ (P / π). Promień okręgu z obwodu: jeśli znasz obwód L, promień wynosi r = L / (2π).
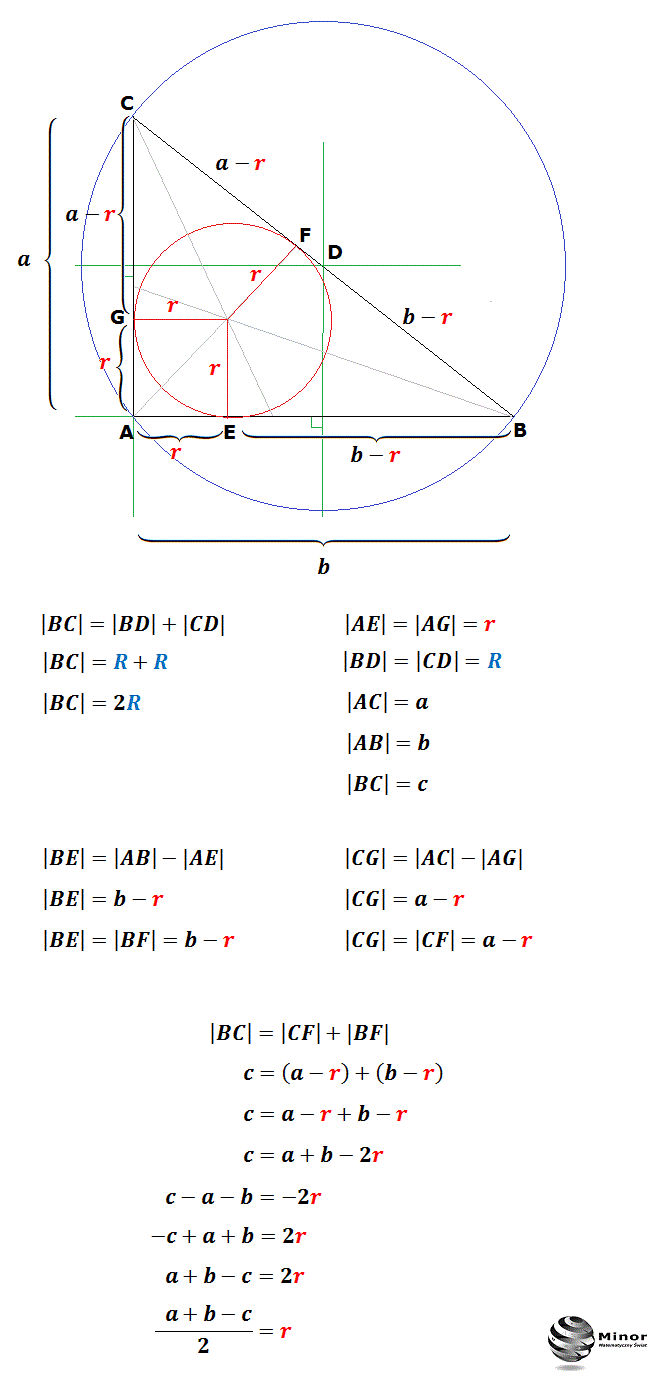
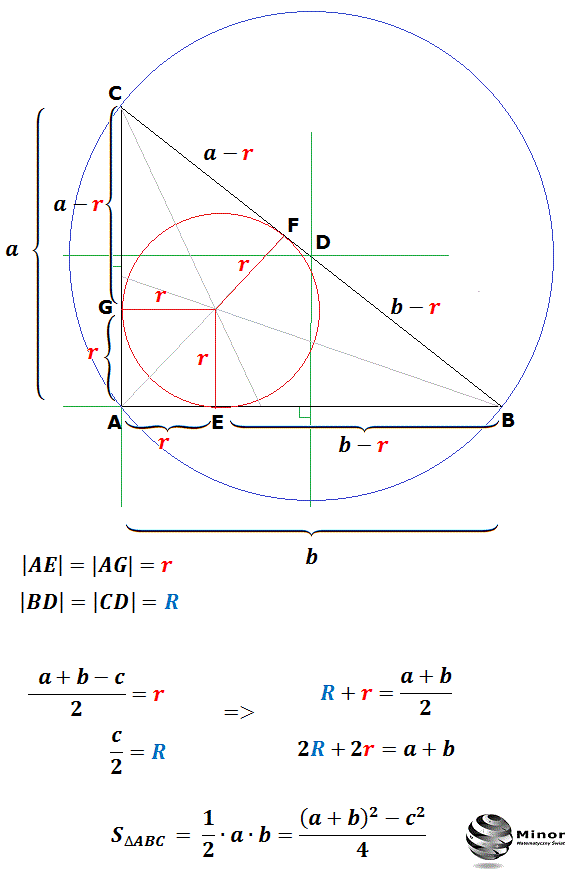
Wzór na promień okręgu wpisanego w trójkąt. Środek okręgu wpisanego w trójkąt znajdujemy rysując dwusieczne kątów trójkąta. Wzory na promień okręgu opisanego na trójkącie. Środek okręgu opisanego na trójkącie znajdujemy rysując symetralne boków trójkąta.
Okrąg Wpisany W Trójkąt Prostokątny Wzory Margaret Wiegel
Materiał ze strony http://matematyka.pisz.pl/strona/876.htmlWyprowadzenie wzoru na promień okręgu wpisanego w czworokąt. Promień to odległość między środkiem okręgu koła, a jego brzegiem. r - to oznaczenie promienia. Cięciwa to odcinek, którego końce leżą na okręgu. Cięciwy mają różne długości. Średnica to najdłuższa cięciwa przechodząca przez środek koła lub okręgu. d - to oznaczenie średnicy. Tak jak to zostało pokazane na.




