LEKTURY na egzaminie; POWTÓRKA Z POLSKIEGO. Antyk (Powtórka) „Biblia" (Powtórka) Średniowiecze (Powtórka) Renesans (Powtórka) Barok (Powtórka). Bryły - podstawowe wzory. H - wysokość bryły P p - pole podstawy P b - pole powierzchni bocznej V - objętość bryły P - pole powierzchni bryły. Graniastosłup. Kalkulatory obliczają objętości i powierzchnie zwykłych brył trójwymiarowych i także niektóre obliczenia pomocnicze, takie jak określanie przekątnej brył i podobne. Kalkulatory sześcian V = a ⋅ a ⋅ a = a 3 P = 6 ⋅ a ⋅ a = 6 ⋅ a 2 prostopadłościan V = a b c P = 2 ⋅ ( a b + a c + b c) walec V = π r 2 h P = 2 ⋅ π r ( r + h) stożek
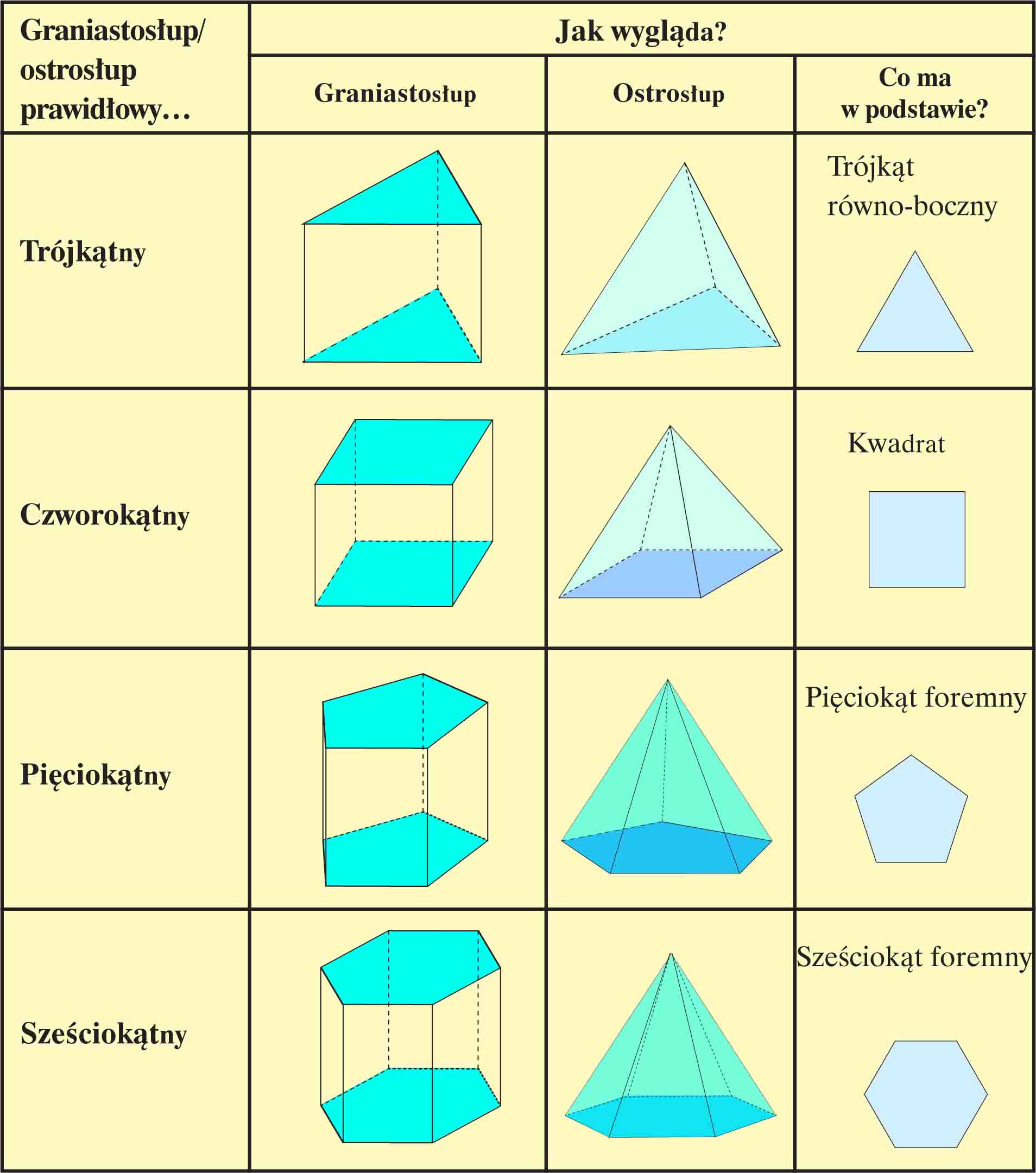
Stereometria AleKlasa
Kula r V = 4 3 π r 3 Chcesz dowiedzieć się więcej o obliczaniu objętości kuli? Obejrzyj ten film. Ucz się za darmo matematyki, sztuki, programowania, ekonomii, fizyki, chemii, biologii, medycyny, finansów, historii i wielu innych. Bryły w trzech wymiarach | 6. klasa | Matematyka | Khan Academy. 6. klasa 11 rozdziałów · 148 umiejętności. Rozdział 1 Stosunki. Rozdział 2 Arytmetyka na liczbach wymiernych. Rozdział 3 Tempa zmian i wartości wyrażone w procentach. Rozdział 4 Potęgowanie i kolejność wykonywania działań. Rozdział 5 Liczby ujemne. Wzory, zadania maturalne i rozwiązania dotyczące brył obrotowych. Jak obliczać objętość i pole całkowite brył? Napisz sprawdzian na 5! Bryły - Spis treści Prostopadłościan Sześcian Graniastosłup Ostrosłup Walec Stożek Kula Zamiana jednostek sześciennych Graniastosłup, prostopadłościan i sześcian - zadania Ostrosłup - zadania Stożek - zadania Pole prostok ta = dlugość. dlugo ⋅ szerokość. szeroko = 1, 5 ⋅ 5 = 7, 5. Te dwie ściany mają w sumie pole powierzchni równe 2 ⋅ 7, 5 = 15 . Dodajmy teraz pola powierzchni wszystkich ścian, aby obliczyć w ten sposób całkowite pole powierzchni tego prostopadłościanu: Pole powierzchni = 12 + 40 + 15 = 67. Pole powierzchni.
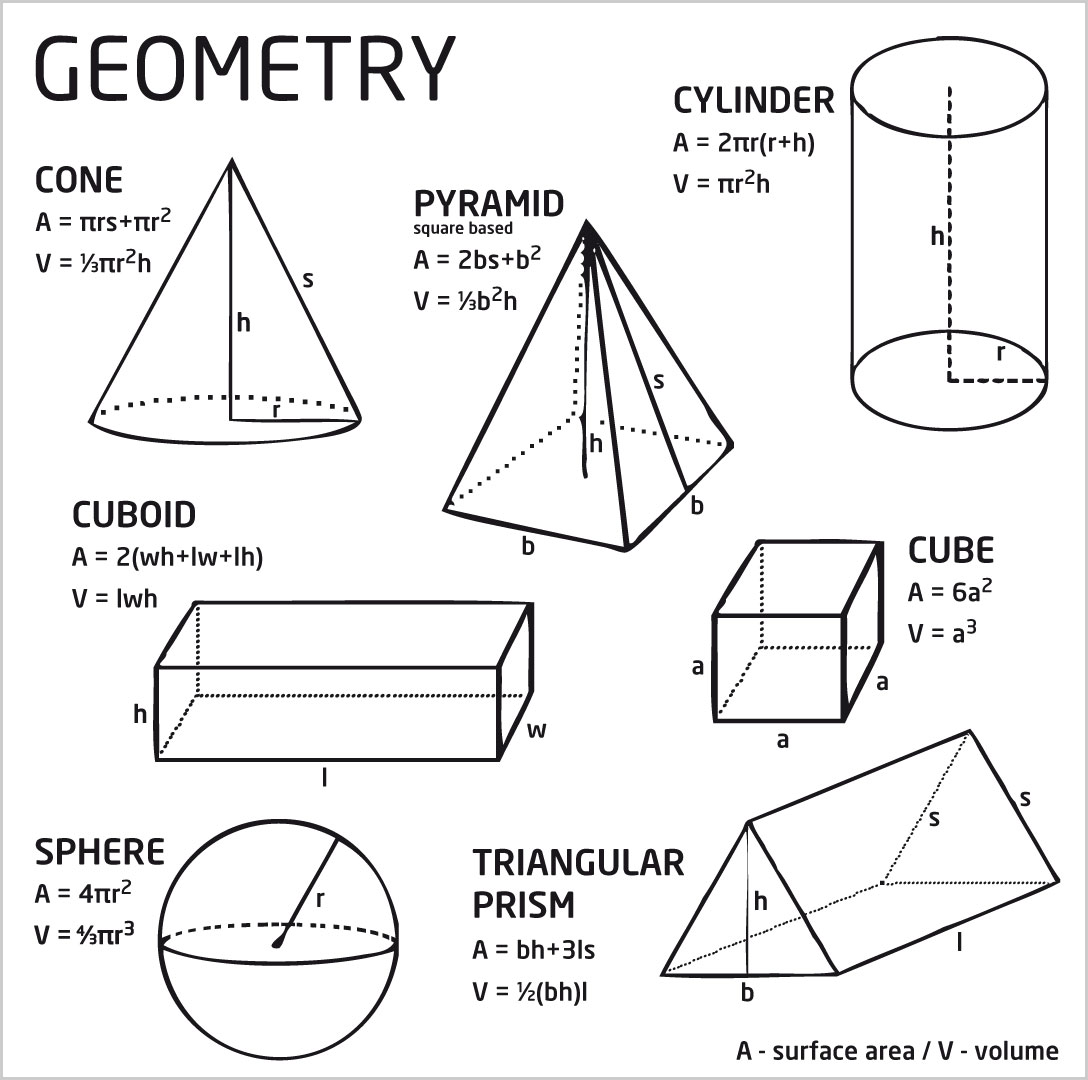
Figury Geometryczne Przestrzenne My XXX Hot Girl
Złożone figury czy bryły można często rozłożyć na prostsze kształty, których środek masy możemy wyznaczyć z ich symetrii.Możemy też uzupełniać figury tak, by miały większą symetrię, dzięki czemu łatwiej będzie wyznaczyć położenie ich środka masy, a wkład od dodanego elementu trzeba po prostu od sumy odjąć.. Definicja bryły obrotowej. Bryła obrotowa - to bryła geometryczna ograniczona powierzchnią powstałą w wyniku obrotu figury płaskiej dookoła prostej (nazywanej osią obrotu ). Nasz kalkulator pomoże ci obliczyć objętość kuli, walca, sześcianu, stożka i brył prostokątnych. Co to objętość? - Definicja objętości Objętość to miara przestrzeni, którą zajmuje dany obiekt lub substancja. Objętość pojemnika jest często rozumiana jako jego pojemność — a nie ilość miejsca, które pojemnik sam zajmuje. Bryły lub kształty 3D. Temat nadrzędny: Geometria. Geometria Matematyka Bryły Stożek Sześcian Prostopadłośc. Walec Graniastosłup Ostrosłup Sfera Powierzchnia Objętość. Dowolny typ zasobu.

EduTab Matematyka WZORY na pola obwody objętości 7018918600
Wzory na objętość brył Jak obliczyć objętość danej figury geometrycznej przestrzennej? Najczęściej obliczanie objętości sprowadza się do zastosowania odpowiedniego wzoru. W poniższej tabeli zawarto podstawowe wzory na objętość brył: Tablica objętości brył Bryły. 12.1 Graniastosłup prawidłowy. Popularne. 12.2 Ostrosłup prawidłowy. 12.3 Obliczanie pól powierzchni i objętości graniastosłupa prostego. 12.4 Obliczanie pól powierzchni i objętości ostrosłupa. 12.5 Obliczanie pól powierzchni i objętości walca. 12.6 Obliczanie pól powierzchni i objętości stożka.
Wzór na pole powierzchni. Nasz kalkulator pola powierzchni może obliczyć pole powierzchni siedmiu różnych brył. Wzór zależy od rodzaju bryły geometrycznej. Pole powierzchni kuli: P = 4πr², gdzie r oznacza promień kuli. Pole powierzchni sześcianu: P = 6a², gdzie a oznacza długość boku. Pole powierzchni walca: P = 2πr². Pola i objętości brył 76% 4334 głosów Treść Grafika Filmy Komentarze 1. Sześcian P=6*a do 2 V=a do 3 2. Prostopadłościan P=2 (a*b+b*h+a*h) V=a*b*h 3. Graniastosłup P=2*Pp+Pb V=Pp*H 4. Ostrosłup P=Pp+Pb V=1/3Pp*h 5. Czworościan foremny Pc= 4Pp = a kwadrat * pierwiastek z 3 V=1/3Pp*h 6. Walec Pc=2*Pp+Pb V=PIr2 (kwadrat)*H 7. Kula Pc=4piR2 (kwadrat)

Bryły podstawowe wzory AleKlasa
Wzór na objętość sześcianu: V = a3. Podobnie jak w każdym prostopadłościanie tak i tu mnożymy 3 wymiary bryły: długość razy szerokość razy wysokość. Pole powierzchni całkowitej sześcianu obliczamy ze wzoru: Pc = 6 ⋅a2. Sześcian składa się z 6 jednakowych kwadratów stąd otrzymaliśmy powyższy wzór. Wzór na pole. Dynamika bryły sztywnej wzory i analiza Bryła sztywna - ciało, którego punkty nie przemieszczają się względem siebie. W ruchu obrotowym bryły sztywnej każdy punkt bryły zatacza okrąg o środku leżącym na osi obrotu bryły. Odległość punktu od osi obrotu (oznaczane jako r) - to najkrótszy odcinek łączący punkt i oś obrotu.



