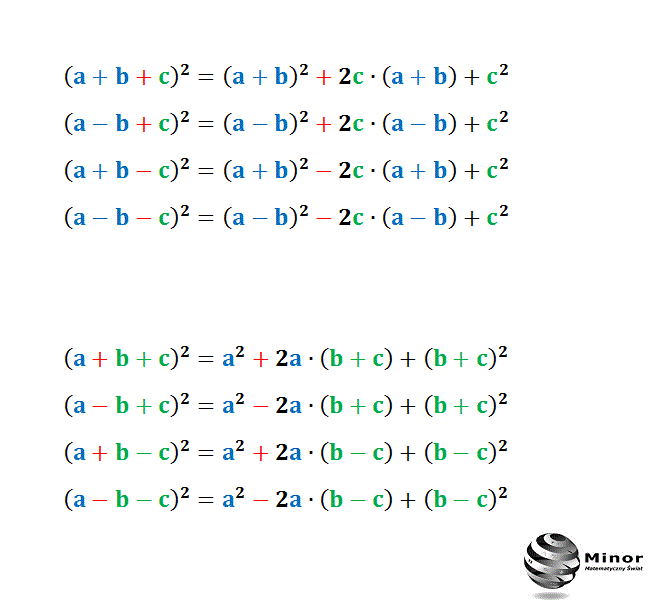Wzory skróconego mnożenia 1. Najważniejsze wzory skróconego mnożenia 2. 3. 4. 5. 6. 7. 8. 9. Zadania ze wzorów skróconego mnożenia Najważniejsze wzory skróconego mnożenia Wzory skróconego mnożenia pozwalają szybciej wykonywać obliczenia. Oto najczęściej stosowane wzory: Wzory skróconego mnożenia - zestaw tożsamości algebraicznych zawierających wyrażenia takie jak: potęgi skończonych sum i różnic: ; sumy i różnice potęg: gdzie wykładnik jest liczbą naturalną. Najprostsze przykłady to te dla wykładnika dwa [1] : kwadrat sumy i różnicy: różnica kwadratów:
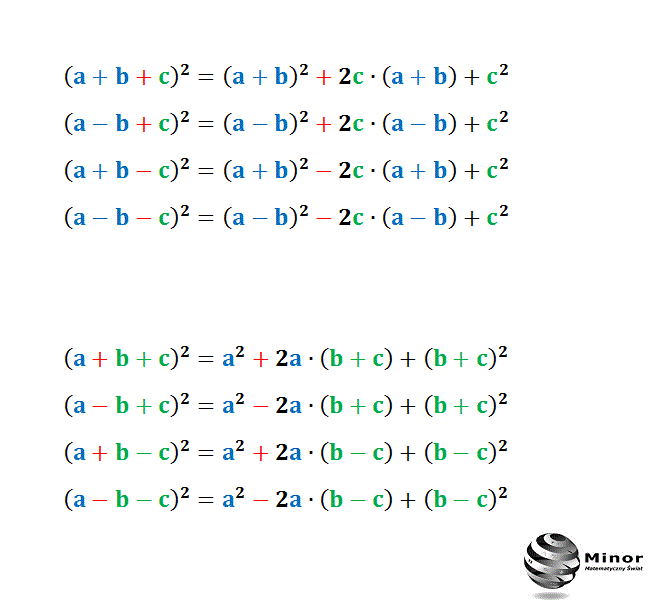
Matematyka
Kwadrat sumy dwóch wyrażeń równy jest sumie trzech składników: pierwszego wyrażenia podniesionego do kwadratu, podwojonego iloczynu tych wyrażeń oraz kwadratu drugiego wyrażenia. Zadanie 1 Korzystając ze wzoru na kwadrat sumy oblicz poniższe wyrażenia: ROZWIĄZANIE: Zadanie 2 Oblicz: ROZWIĄZANIE: Zadanie 3 Zadanie 1. matura 2024 PP Liczba (2 − 3 2-√)2 jest równa A. −14 B. 22 C. −14 − 12 2-√ D. 22 − 12 2-√ Film Youtube Odp Zadanie 2. matura 2024 PP Wartością wyrażenia (3 − 5-√)2 jest liczba A. 14 + 6 6-√ B. 4 − 6 5-√ C. 14 − 6 5-√ D. 4 Film Youtube Odp Zadanie 3. matura 2024 PP Dla każdej liczby rzeczywistej x, wyrażenie 4x2 − 12x + 9 jest równe Wzory skróconego mnożenia to takie wzory, które umożliwiają nam szybsze obliczenia na liczbach oraz wyrażeniach algebraicznych. Na poziomie podstawowym posługujemy się przede wszystkim trzema następującymi wzorami: 17K Share Save 649K views 11 years ago ALGEBRA RÓWNANIA NIERÓWNOŚCI UKŁADY RÓWNAŃ ŁATWY DOSTĘP do wszystkich moich lekcji z matematyki uzyskasz: 1. Poprzez moją aplikację na Androida.

Wzory skróconego mnożenia Demotywatory.pl
Kurs maturalny z matematyki - zakres podstawowy:http://www.matspot.pl/matura/matura_kurs.htmlzobacz też:http://www.matspot.pl/https://www.facebook.com/mathspot/ Podnoszenie do kwadratu dwumianów o postaci (x+a)². Wzory skróconego mnożenia: różnica kwadratów. Podnoszenie do kwadratu dwumianów za pomocą wzorów skróconego mnożenia. Szczególne iloczyny postaci (ax+b) (ax-b) Podnoszenie do kwadratu dwumianów o postaci (ax+b)². Szczególne iloczyny dwumianów, przypomnienie. >. Algebra 1 >. Ta playlista dotyczy wzorów skróconego mnożenia dla drugich potęg. Poznasz, nauczysz się stosować oraz zobaczysz, skąd biorą się wzory skróconego mnożenia na kwadrat sumy, kwadrat różnicy oraz różnicę kwadratów. Dowiesz się, jak wykorzystać te wzory do upraszczania wyrażeń algebraicznych, rozwiązywania zadań dowodowych oraz usuwania niewymierności z mianownika. Odsłon: 687 Wzory skróconego mnożenia - definicje, przykłady Watch on Twierdzenie 1 (wzory skróconego mnożenia stopnia drugiego) Dla dowolnych wyrażeń a, b prawdziwe są wzory: kwadrat sumy kwadrat różnicy różnica kwadratów Przykład 1 Oblicz bez użycia kalkulatora: Przykład 2 Wykonaj działania: Przykład 3 Rozłóż dane wyrażenia na czynniki:

Matematyka Bliżej nas WZORY SKRÓCONEGO MNOŻENIA ROZWIJAMY SIĘ
Wprowadzanie do rozkładania pełnych kwadratów na czynniki. Rozkładanie wyrażeń kwadratowych na czynniki: wzory skróconego mnożenia. Wykorzystanie wzorów skróconego mnożenia. Przykład - rozkład trójmianu będącego kwadratem dwumianu. Rozpoznawanie kwadratu dwumianu w trójmianie kwadratowym. Przykład - rozkład na czynniki w. zobacz też:http://www.matspot.pl/https://www.facebook.com/mathspot/
Wzory skróconego mnożenia przyspieszają przekształcanie wyrażeń algebraicznych. Kwadrat sumy (a + b)2 = a2 + 2ab + b2 Kwadrat różnicy (a − b)2 = a2 − 2ab + b2 Różnica kwadratów a2 − b2 = (a − b)(a + b) Sześcian sumy (a + b)3 = a3 + 3a2b + 3ab2 + b3 Sześcian różnicy (a − b)3 = a3 − 3a2b + 3ab2 − b3 Suma sześcianów a3 + b3 = (a + b)(a2 − ab + b2) 1. Podstawowe wzory skróconego mnożenia Omawianie tego tematu, zaczniemy od krótkiego ćwiczenia: Ćwiczenie 1: Przedstaw wyrażenia w postaci sumy algebraicznej: a) b) c) d) e) f) g) h) i) Rozwiązania i odpowiedzi: a) Suma algebraiczna to wyrażenie w którym pomiędzy poszczególnymi jednomianami występują tylko działania oraz .

Wzory skróconego mnożenia, trójkąt Pascala
Wzory skróconego mnożenia. Wzory skróconego mnożenia przydatne są podczas przekształceń wyrażeń algebraicznych, często ułatwiają rachunki. Czasem są bardziej przydatne, gdy stosujemy je "w drugą stronę", aby z pewnego wyrażenia otrzymać np. kwadrat sumy. Mają zastosowanie przy rozwiązywaniu równań, znajdowaniu pierwiastków. Zastosowanie wzorów skróconego mnożenia - przykłady Analizując przykłady zawarte w tym materiale, poznasz wzory skróconego mnożenia drugiego stopnia. Zapiszesz kwadrat dwumianu oraz iloczyn dwóch takich samych wyrażeń w postaci sumy algebraicznej. Przykład 1 Zapisz iloczyn w postaci sumy. 3 a + 2 3 a + 2 2 + 4 x 2 + 4 x x + y x + y