Объем параллелепипеда равен произведению площади основания на высоту. Формула объема параллелепипеда: V = So · h где V - объем параллелепипеда, So - площадь основания, h - длина высоты. Смотрите также онлайн калькулятор для расчета объема параллелепипеда Объем прямоугольного параллелепипеда 11:27 Формулы объемов и площадей геометрических фигур Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах.

Как легко запомнить формулы объемов?
Куб Куб есть параллелепипедом, все ребра (стороны) которого равны. Если длина стороны куба равна a, тогда формула объема: \displaystyle V = a.a.a = a^3 V = a.a.a = a3 Площадь поверхности: \displaystyle S = 6a \cdot a = 6a^2 S = 6a⋅a =6a2 Параллелепипед Параллелепипед это фигура, все стороны которой - параллелограммы. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright. Формула площади. Объем правильного тетраэдра Объем конуса Какая форма лучше для маленького (2-3 куб см) ценного абстрактного предмета? Возможно, шар, куб, пирамида или что-то другое? Объем призмы Объем прямоугольной призмы Объем прямоугольной призмы Найти ребро куба, зная объем Вписанная и описанная сфера куба Доаказетльство формулы диагонали куба Объём (геометрия) Объём — это аддитивная функция от множества ( мера ), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без.
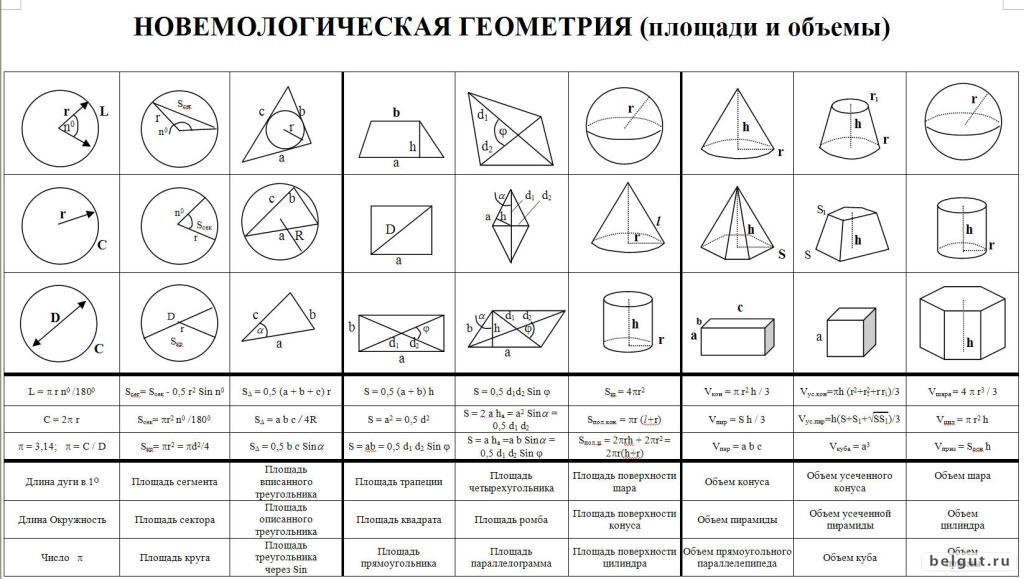
Площади и объемы плоских фигур » Фото БелГУТа
Объем геометрических фигур. Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид). Данная статья содержит. Объем и площадь фигур Калькуляторы выполняют расчеты объема и площади трехмерных геометрических фигур, а также некоторые вспомогательные вычисления, такие как определение диагонали геометрических фигур, и т.п. Калькуляторы куб V = a ⋅ a ⋅ a = a 3 S = 6 ⋅ a ⋅ a = 6 ⋅ a 2 прямоугольный параллелепипед V = a b c S = 2 ⋅ ( a b + a c + b c) цилиндр V = a 3 , где V — объем куба, a - длина грани куба. Объём призмы Призма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Объем призмы равен произведению площади основания призмы, на высоту. Выберите необходимый онлайн калькулятор, введите известные величины и калькулятор поможет вам вычислить объем. Онлайн калькуляторы. Объем геометрических фигур. Объем куба Объем призмы.

Объемы и площади всех фигур Формулы объемов и площадей геометрических фигур — Таловская средняя
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам нужно будет знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр. Объемы фигур; Расчет объема куба, пирамиды, конуса, цилиндра, шара (объема всех фигур). Объемы фигур: Основные свойства кругового конуса
Объемы фигур. Объем конуса. Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. V = abc Объем призмы V = Sоснования ⋅ H Объем пирамиды V = 1 3Sоснования ⋅ H Объем шара Vшара = 4 3πR3 R - радиус Объем цилиндра V = πR2H R - радиус основания

Объем, площадь геометрических фигур
В данном разделе можно рассчитать стороны, углы, площади, периметры и объемы всех геометрических фигур, а также вычислить определенные величины, свойственные конкретному ряду фигур. Здесь. Воспользуйтесь калькуляторами расчета объема геометрических фигур, тел, объектов — рассчитайте онлайн объем в м3, см3, литрах и других единицах. Калькуляторы объема от КАЛК.ПРО.




