Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объем и площадь фигур — онлайн калькуляторы, формулы, расчеты Объем и площадь фигур Калькуляторы выполняют расчеты объема и площади трехмерных геометрических фигур, а также некоторые вспомогательные вычисления, такие как определение диагонали геометрических фигур, и т.п. Калькуляторы куб V = a ⋅ a ⋅ a = a 3 S = 6 ⋅ a ⋅ a = 6 ⋅ a 2

Картинки по запросу все формулы геометрии Стереометрия, Математические блокноты, Математика
Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. Формула объема параллелепипеда: V = So · h где V - объем параллелепипеда, So - площадь основания, h - длина высоты. Смотрите также онлайн калькулятор для расчета объема параллелепипеда Объем прямоугольного параллелепипеда Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. 1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: 2) Она также равна половине произведения его сторон на синус угла между ними: 3) По формуле Герона, полупериметр. 4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr. 5) Еще один способ. Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π. Формула площади боковой поверхности конуса: S = π R l Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности. Формула площади полной поверхности конуса:

Как легко запомнить формулы объемов?
Формулы площадей и объёмов геометрических фигур,объем,площадь,формула,шпаргалки,куб,многогранник,параллелепипед,пирамида,конус.. картинки для учеников и студентов с формулами площадей. Площади геометрических фигур. Площадь квадрата. 0361. Квадрат - это параллелограмм, у которого все углы и все стороны равны. а - сторона квадрата A, B, C. Площади геометрических фигур. Площадь. Статья подробно разбирает формулы и методы для вычисления все площади фигур: квадрата, прямоугольника, параллелограмма, треугольника, трапеции, круга и других. Рассматриваются свойства площадей, задачи на площади. Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии.Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части.
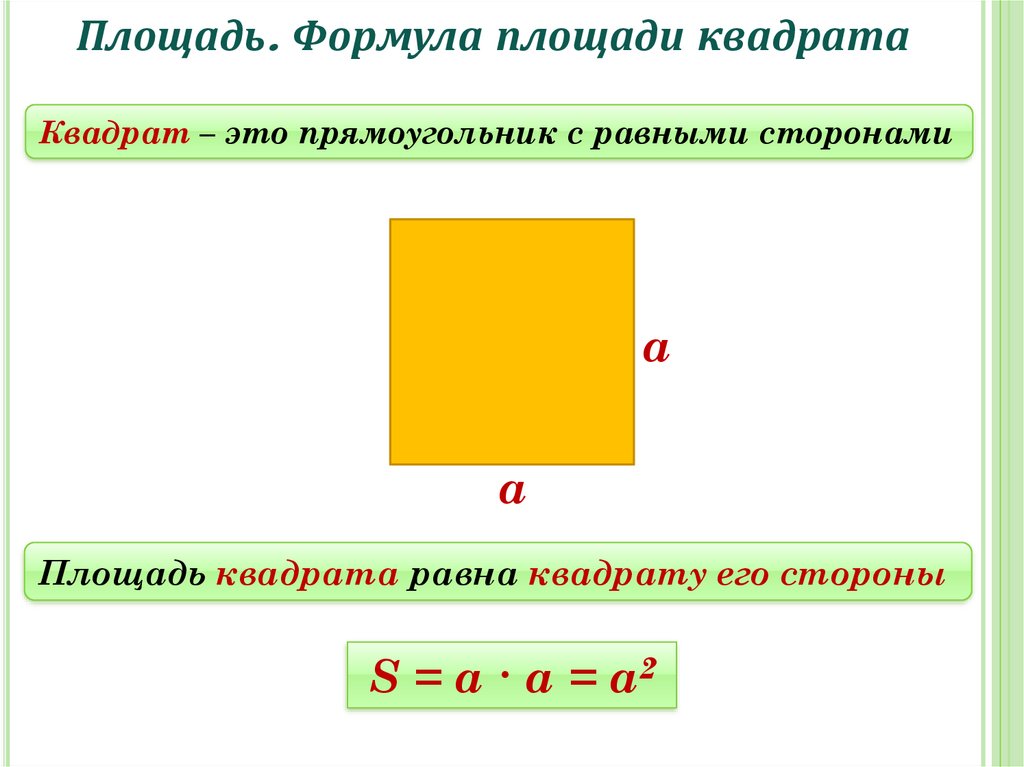
Площади и объемы геометрических фигур online presentation
Площадь, Формулы площади, Формула площади, Формулы площади плоских фигур, Формулы площади треугольника, Формулы площади поверхности объемных тел, формула площади поверхности Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов.
Общая площадь поверхности = πr 2 + πrs Чтобы найти объем шара, вам нужны только радиус и высота. Объем = 1/3 πr 2 ч 03 из 16 В таблице 1 приведены наиболее употребительные формулы для расчета площади, объема и периметра. Вычисление длин и площадей плоских фигур. - число сторон правильного многоугольника. - радиус.

Задания по теме Формулы. Площади и объемы фигур"(5 класс)
Для определения площади поверхности такого цилиндра используется формула: S = 2 pi × R × (R + h), где R — радиус основания, h — высота цилиндра. Для вычисления объема цилиндра геометры применяют. Площадь фигуры равна сумме площадей фигур, из которых она состоит. 2. Равные фигуры имеют одинаковые объемы. Объем фигуры равен сумме объемов фигур, из которых она состоит. 3.




