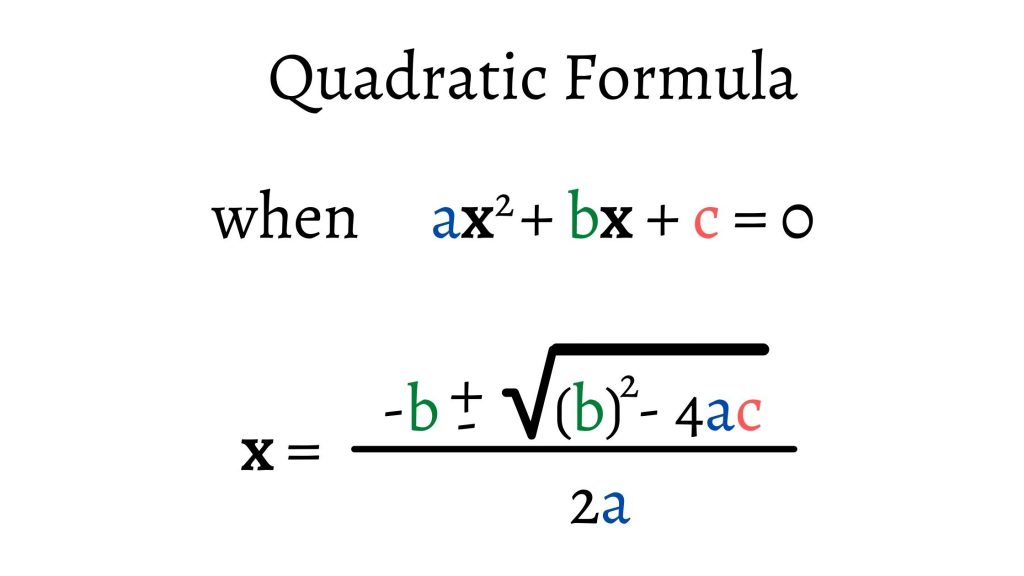The standard form of a quadratic equation is: ax 2 + bx + c = 0, where a, b and c are real numbers and a != 0 The term b 2; - 4ac is known as the discriminant of a quadratic equation. It tells the nature of the roots. If the discriminant is greater than 0, the roots are real and different. The quadratic equation is represented by ax + bx + c ,, and are real numbers and constants, and a ≠ 0. The root of the quadratic equations is a value of that satisfies the equation. The Discriminant is the quantity that is used to determine the nature of roots: Discriminant (D) = b. Based on the nature of the roots, we can use the given.
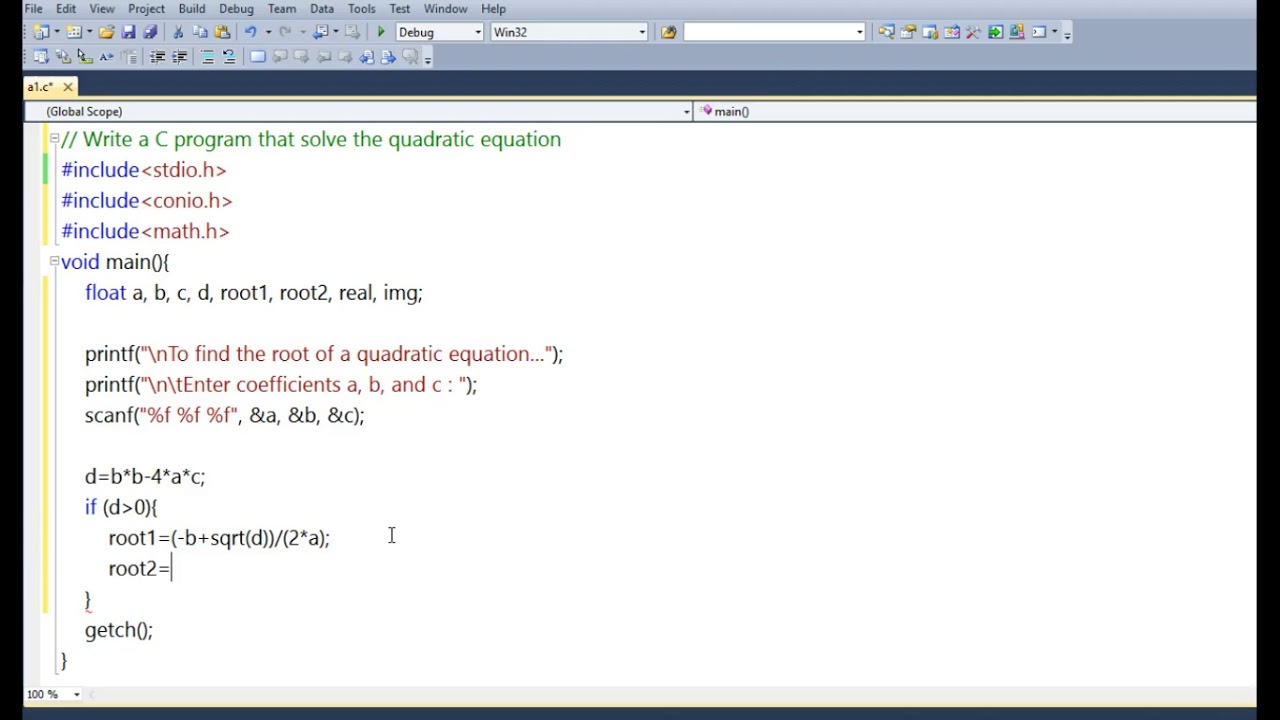
C Program Quadratic equation YouTube
A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared. The standard form of the quadratic equation is ax² + bx + c = 0 where a, b, and c are real and a !=0, x is an unknown variable. The nature of roots is determined by the discriminant. Solving quadratic equations or finding the roots of equations of second degree is a popular problem in many programming languages. The equations of second degree which resemble the standard form: ax 2 +bx+c=0, are known as quadratic equations. A large number of quadratic equations need to be solved in mathematics, physics and engineering. For a quadratic equation ax2+bx+c = 0 (where a, b and c are coefficients), it's roots is given by following the formula. Formula to Find Roots of Quadratic Equation The term b 2 -4ac is known as the discriminant of a quadratic equation. The discriminant tells the nature of the roots. ax 2 + bx + c = 0 But sometimes a quadratic equation does not look like that! For example: How To Solve Them? The " solutions " to the Quadratic Equation are where it is equal to zero. They are also called " roots ", or sometimes " zeros " There are usually 2 solutions (as shown in this graph).

Algebra I Vazquez October 2013
In algebra, a quadratic equation (from Latin quadratus ' square ') is any equation that can be rearranged in standard form as [1] where x represents an unknown value, and a, b, and c represent known numbers, where a ≠ 0. (If a = 0 and b ≠ 0 then the equation is linear, not quadratic.) . Then we plug a , b , and c into the formula: x = − 4 ± 16 − 4 ⋅ 1 ⋅ ( − 21) 2 The quadratic formula helps us solve any quadratic equation. First, we bring the equation to the form ax²+bx+c=0, where a, b, and c are coefficients. Then, we plug these coefficients in the formula: (-b±√ (b²-4ac))/ (2a) . See examples of using the formula to solve a variety of equations. Created by Sal Khan. Questions Tips & Thanks [Why is this a quadratic equation?] This is a product of two expressions that is equal to zero. Note that any x value that makes either ( x − 1) or ( x + 3) zero, will make their product zero. ( x − 1) ( x + 3) = 0 ↙ ↘ x − 1 = 0 x + 3 = 0 x = 1 x = − 3

C Program To Find Quadratic Equation truemfile
Learning Objectives In this section, you will: Solve quadratic equations by factoring. Solve quadratic equations by the square root property. Solve quadratic equations by completing the square. Solve quadratic equations by using the quadratic formula. Figure 1 How do you calculate a quadratic equation? To solve a quadratic equation, use the quadratic formula: x = (-b ± √ (b^2 - 4ac)) / (2a). What is the quadratic formula? The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √ (b^2 - 4ac)) / (2a) Does any quadratic equation have two solutions?
The solutions to the quadratic equation, as provided by the Quadratic Formula, are the x-intercepts of the corresponding graphed parabola. How? Well, when y = 0, you're on the x-axis. The x-intercepts of the graph are where the parabola crosses the x-axis. You're applying the Quadratic Formula to the equation ax 2 + bx + c = y, where y is set. A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form.
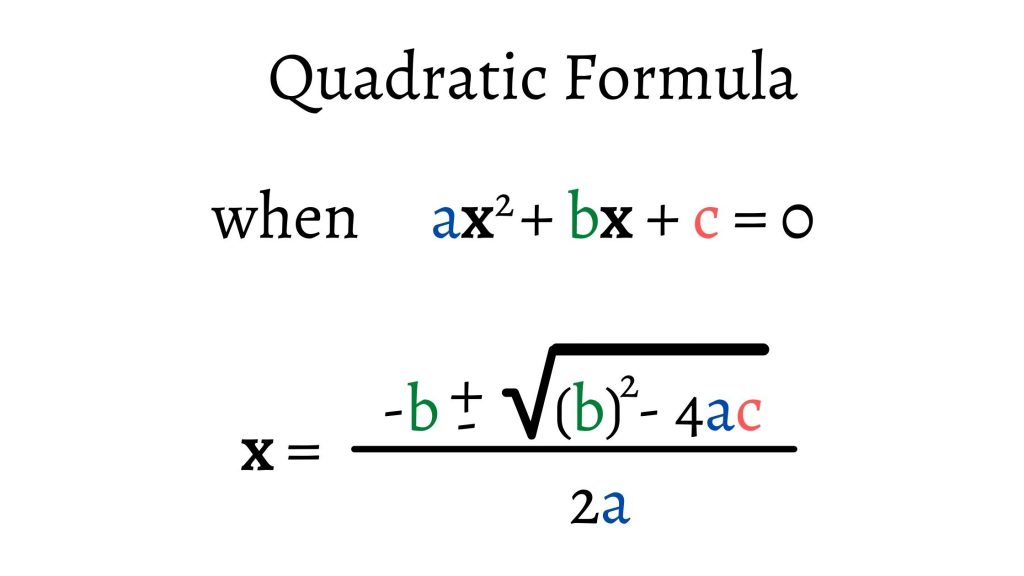
The Quadratic Formula. Its Origin and Application IntoMath
This online calculator is a quadratic equation solver that will solve a second-order polynomial equation such as ax 2 + bx + c = 0 for x, where a ≠ 0, using the quadratic formula. The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots. Explore the Quadratic Equation. A Quadratic Equation. ( a, b, and c can have any value, except that a can't be 0.) Try changing a, b and c to see what the graph looks like. Also see the "roots" (the solutions to the equation). Then read more about the Quadratic Equation.