Запишем уравнение бегущей волны, зная, что она плоская: Используем в записи уравнения w=, запишем (1.1) в начальный момент времени (t=0): Из условий задачи известно, что в начальный момент. Частные случаи. Стоячая волна является частным случаем бегущей волны с =, где — групповая скорость волны.. То есть, две одинаковые периодические бегущие волны (в рамках справедливости принципа суперпозиции.

Продольные и поперечные волны. Уравнение плоской гармонической волны. Стоячие волны
Уравнение бегущей волны. Колебательное движение тела в упругой среде является источником механической волны. Волну, переносящую энергию, называют бегущей волной. Тема урока: Упругие механические волны. Уравнение бегущей и стоячей волны С понедельника по пятницу с 09:00-18:. Уравнение плоской бегущей волны Чтобы описать волновое движение, нужно найти амплитуды и фазы. Уравнение бегущей волны (10.1) можно записать следующим образом: 22 sin sin sin sin x A tAtxAtxAt T x Фронты плоской волны в трёхмерном пространстве и вектор фазовой скорости. Пло́ская волна́ — волна, поверхность постоянной фазы которой представляет собой плоскость. Фронт плоской волны.

Распространение волн в упругих средах. Уравнение гармонической бегущей Колебания волны и волны
Уравнение бегущей волны. Рассмотрим колебания источника волны, происходящие с циклической частотой ω \(\left(\omega =2\pi \cdot \nu =\dfrac{2\pi }{T} \right)\) и амплитудой A: Фронт бегущей волны перемещается с течением времени вдоль оси х с фазовой скоростью v. Такие волны называются плоскими.. Но волновое уравнение (2.70) имеет и другие решения, нежели плоские. Уравнение бегущей волны. Бегущие волны - это волны, несущие энергию в пространстве. Передача энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический.
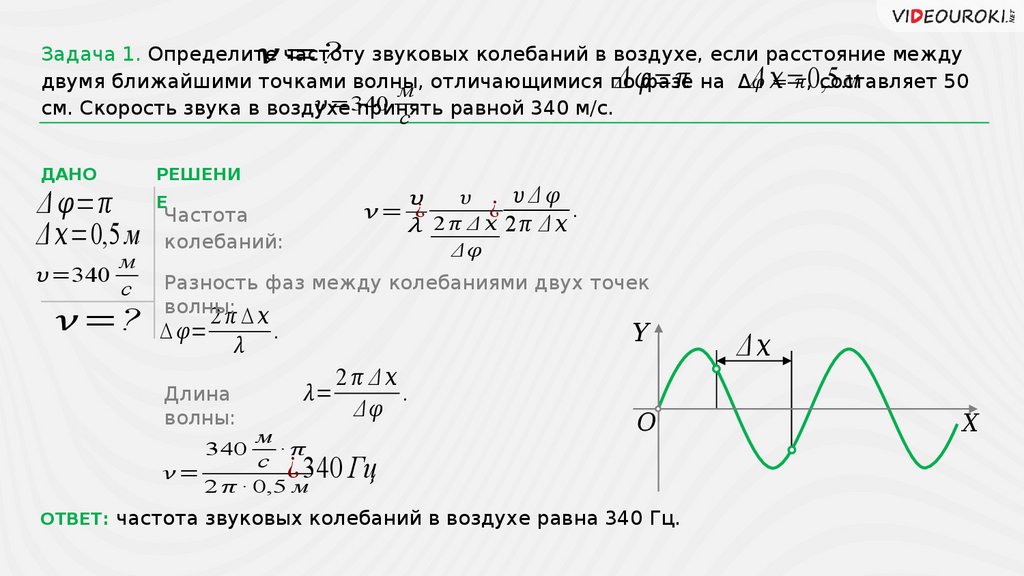
Распространение волн в упругих средах. Уравнение гармонической бегущей Колебания волны и волны
Уравнение бегущей волны. Колебательное движение тела в упругой среде является источником механической волны. Волну, переносящую энергию, называют бегущей волной. efizika, ефизика, efizika.ru, Flash, анимации, модели, демонстрации, дистанционное обучение физике, электронное обучение физике, медиаматериалы по физике, медиадидактика, математическое моделирование в физике, лабораторные.
Конспект урока "Распространение волн в упругих средах. Уравнение гармонической бегущей волны". Всё время, пока существует волна, частицы среды совершают колебания около своих положений. На простом примере получаем уравнение плоской бегущей (в положительном направлении оси) волны. Вводится.

Распространение волн в упругих средах. Уравнение гармонической бегущей Колебания волны и волны
Уравнение гармонической бегущей волны можно записать в виде: s = smsin (ωt - kx), где k — волновое число. Фазы колебаний двух точек, находящихся на расстоянии λ, отличаются на 2π, то есть колебания. 4. Волновые процессы. Продольные и поперечные волны. 5. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение. Принцип суперпозиции . 1. Гармонические колебания и их характеристики




