Условие параллельности двух прямых, угловые коэффициенты, формулы, уравнение, график, пример с решением Условие параллельности прямых через определитель Если две прямые представлены уравнениями \[ \begin{cases} A_1 x + B_1 y + C_1 = 0 \\ A_1 x + B_1 y + C_1 = 0 \end{cases} \]
XYZ Взаимное расположение прямых на плоскости. Расположение прямых условие параллельности
Условием параллельности двух прямых, заданных уравнениями служит равенство угловых коэффициентов т. е. прямые (1) и (2) параллельны, если угловые коэффициенты равны, и не параллельны, если. Итак, условие (необходимое и достаточное) параллельности прямых заключается в равенстве их угловых коэффициентов. Условие параллельности двух прямых можно получить и непосредственно из формулы (9). В случае перпендикулярности прямых (и только в этом случае) можно считать, что Отсюда следует, что или откуда или окончательно Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b. Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Параллельными прямыми называются прямые, которые лежат в одной плоскости и никогда не пересекаются (на протяжении бесконечности). У параллельных прямых одинаковый угловой коэффициент.

Презентация на тему "Лекционнопрактическое занятие по теме Аналитическая геометрия на
условие параллельности прямых: прямые, заданные уравнениями y=k1x+b1 и y=k2x+b2, параллельны, если их угловые коэффициенты равны: k = k . II. Для общего уравнения прямой угловые коэффициенты Отсюда и получаем условие параллельности для прямых a 1 x+b 1 y+c 1 =0 и a 2 x+b 2 y+c 2 =0: Уравнение прямой Добавить комментарий Отменить ответ Определение: Две прямые на плоскости называются параллельными, если они не пересекаются (Рис. 1). Обозначается это так: . Рис. 1 Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной (Рис. 2). Рис. 2 Следствие1: Если прямая пересекает одну из параллельных прямых, то она пересекает и другую. Рис. 3 Дано:. Все признаки параллельности прямых завязаны на знание свойств углов и теоремы о внешнем угле треугольника. Признак 1. Две прямые параллельны, если накрест лежащие углы равны. Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются и лежат в одной плоскости. Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.

§ 18. Условие параллельности прямых
Параллельные прямые - прямые на плоскости или в пространстве, не имеющие общих точек. Обозначение: a || b. Перпендикулярные прямые - прямые, образующие прямой угол. Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек. Определение. Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек. Определим признаки параллельности двух прямых, связанные с этими парамы углов. Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Уравнение прямой на плоскости презентация онлайн
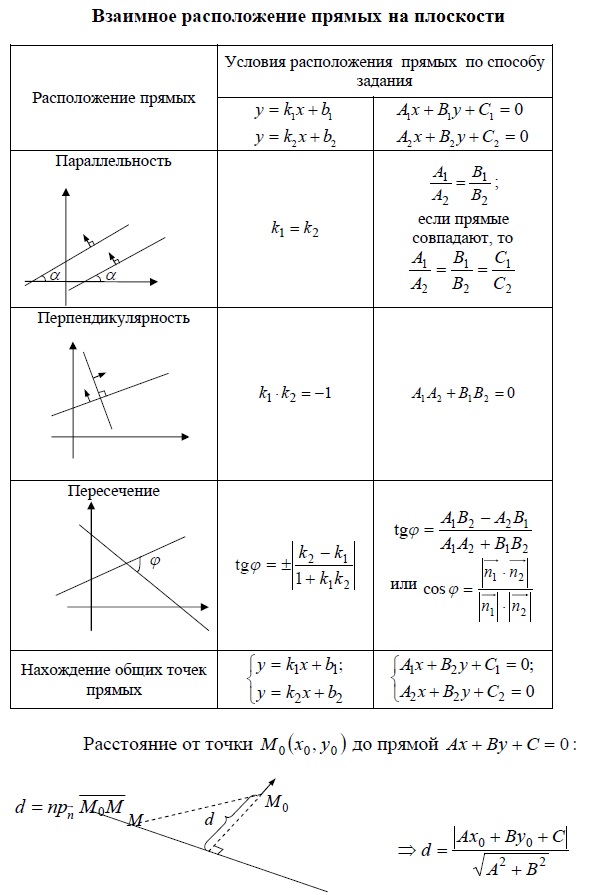
Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости. Расположение прямых - условие параллельности, условие перпендикулярности, условие пересечения по углом φ , нахождение общих точек прямых.




