Özel açılar için: Sin (0°) = 0 Sin (30°) = 1/2 Sin (45°) = 1/√2 Sin (60°) = √3/2 Sin (90°) = 1 Özel Açıların Kosinüs (Cos) Trigonometrik Değerleri Bir dik üçgende bir açının kosinüsü, komşu kenarın uzunluğunun hipotenüsün uzunluğuna oranıdır. Özel açılar için: Cos (0°) = 1 Cos (30°) = √3/2 Cos (45°) = 1/√2 Cos (60°) = 1/2 Cos (90°) = 0 Trigonometry Calculator Created by Hanna Pamuła, PhD Reviewed by Bogna Szyk and Jack Bowater Last updated: Oct 23, 2023 Table of contents: What is trigonometry? Trig calculator finding sin, cos, tan, cot, sec, csc Trigonometry calculator as a tool for solving right triangle FAQ
Các công thức cos sin tan rule thông dụng và áp dụng trong toán học
Trigonometry. Free math problem solver answers your trigonometry homework questions with step-by-step explanations. Trigonometry. Trigonometry is a branch of mathematics concerned with relationships between angles and ratios of lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest. While the basic trigonometric functions like sine, cosine, and tangent are defined in the context of two-dimensional right triangles, they can be generalized to higher dimensions using concepts from linear algebra and vector spaces.. That's not a problem, its a statement. csc(Θ) = 1/sin(Θ), sec(Θ) = 1/cos(Θ), and cot(Θ) = 1/tan(Θ). Because of all that we can say: sin (θ) = 1/csc (θ) cos (θ) = 1/sec (θ) tan (θ) = 1/cot (θ) And the other way around: csc (θ) = 1/sin (θ) sec (θ) = 1/cos (θ) cot (θ) = 1/tan (θ) And we also have: cot (θ) = cos (θ)/sin (θ) Pythagoras Theorem

How to Remember the Trigonometric Table 9 Steps (with Pictures)
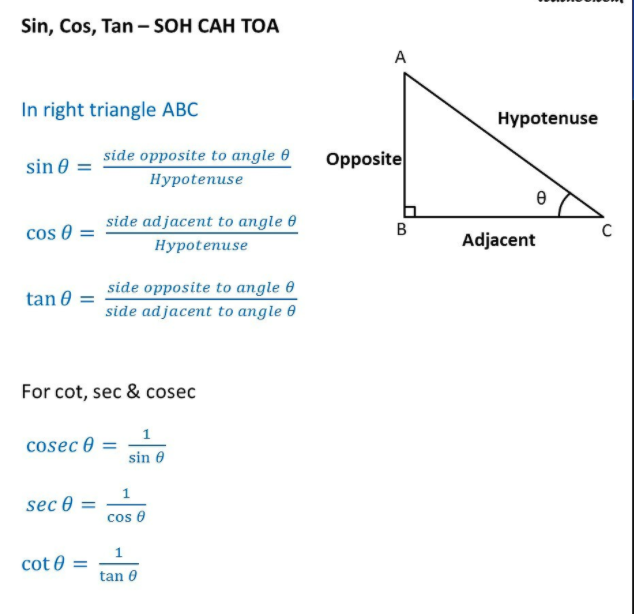
The Trigonometric Identities are equations that are true for Right Angled Triangles. Periodicity of trig functions. Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π. Identities for negative angles. Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions. Values of Trigonometric Ratios for Standard Angles Trigonometric Angles : Table Values of sin, cos, tan, cosec, sec and cot at various degree of angles (0°, 30°, 45°, 60°, 90°, 180°, 270°). Trigonometry is also spelled as Trignometry. Trigonometric ratio / function: cos^2 x + sin^2 x = 1. sin x/cos x = tan x. You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more. some other identities (you will learn later) include -. cos x/sin x = cot x. 1 + tan^2 x = sec^2 x. 1 + cot^2 x = csc^2 x. hope this helped! 1 comment. Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: For a given angle θ each ratio stays the same no matter how big or small the triangle is To calculate them: Divide the length of one side by another side Example: What is the sine of 35°?

Đừng bỏ lỡ Công Thức Lượng Giác Sin, Cos, Tan, Cot đầy đủ và Bí Kíp Học Thuộc Công Thức Lượng
Reduction formulas. (27) sin 2 θ = 1 − cos 2 θ 2. (28) cos 2 θ = 1 + cos 2 θ 2. (29) tan 2 θ = 1 − cos 2 θ 1 + cos 2 θ = sin 2 θ 1 + cos 2 θ = 1 − cos 2 θ sin 2 θ. Fundamental Trigonometric Identities is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts. Algebra (all content) 20 units · 412 skills. Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions. Unit 8 Absolute value equations, functions, & inequalities.
The following (particularly the first of the three below) are called "Pythagorean" identities. sin 2 ( t) + cos 2 ( t) = 1. tan 2 ( t) + 1 = sec 2 ( t) 1 + cot 2 ( t) = csc 2 ( t) Advertisement. Note that the three identities above all involve squaring and the number 1. You can see the Pythagorean-Thereom relationship clearly if you consider. The reciprocal identities are simply definitions of the reciprocals of the three standard trigonometric ratios: (1.8.1) sec θ = 1 cos θ csc θ = 1 sin θ cot θ = 1 tan θ. Also, recall the definitions of the three standard trigonometric ratios (sine, cosine and tangent): (1.8.2) sin θ = o p p h y p cos θ = a d j h y p tan θ = o p p a d y.

Fitfab Sin Cos Tan Table Full
In this case, we add C and D to the general form of the tangent function. f(x) = Atan(Bx − C) + D. The graph of a transformed tangent function is different from the basic tangent function tanx in several ways: FEATURES OF THE GRAPH OF Y = Atan(Bx − C) + D. The stretching factor is | A |. The period is π | B |. Sin, cos, and tan are trigonometric ratios that relate the angles and sides of right triangles. Sin is the ratio of the opposite side to the hypotenuse, cos is the ratio of the adjacent side to the hypotenuse, and tan is the ratio of the opposite side to the adjacent side. They are often written as sin (x), cos (x), and tan (x), where x is an.




