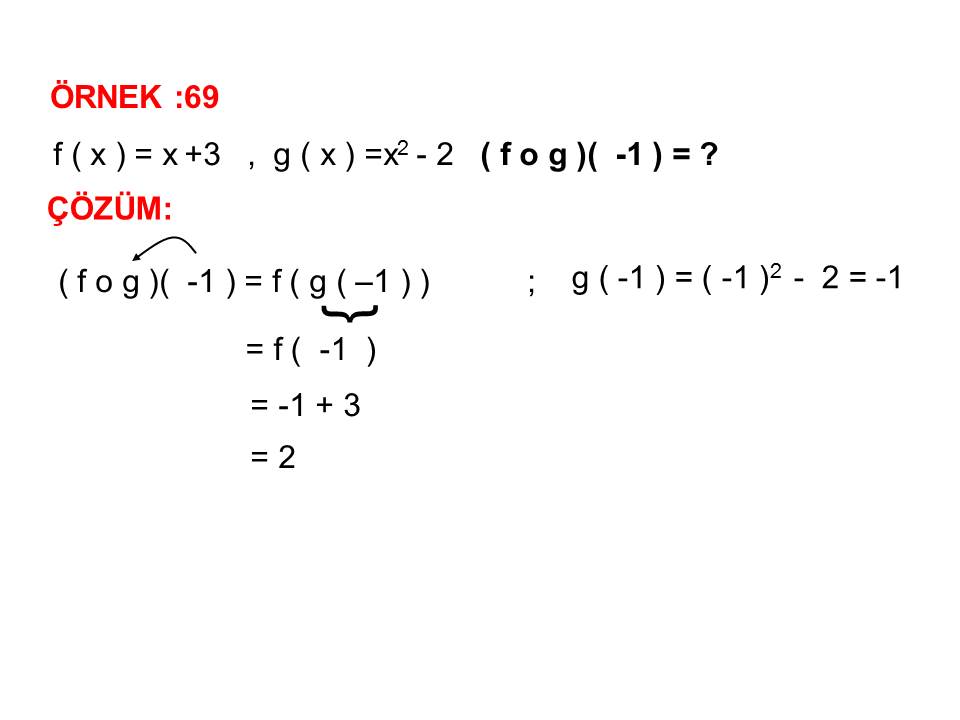Bu İçerik Eşit Fonksiyon Soruları, Eşit Fonksiyon Soru Çözümü, Eşit Fonksiyon Konu Anlatımı, Eşit Fonksiyon Nedir, Eşit Fonksiyon Örnekleri konularını kapsamaktadır. EN SON EKLENEN 9.Sınıf Fonksiyonlar İle İlgili Çözümlü Testi Bu konuda fonksiyon çeşitleri olarak birim fonksiyon, sabit fonksiyon, doğrusal fonksiyon, eşit fonksiyon, tek fonksiyon, çift fonksiyon, parçalı fonksiyon, bire bir fonksiyon, örten fonksiyon ve içine fonksiyon yer almaktadır. BİRİM FONKSİYON
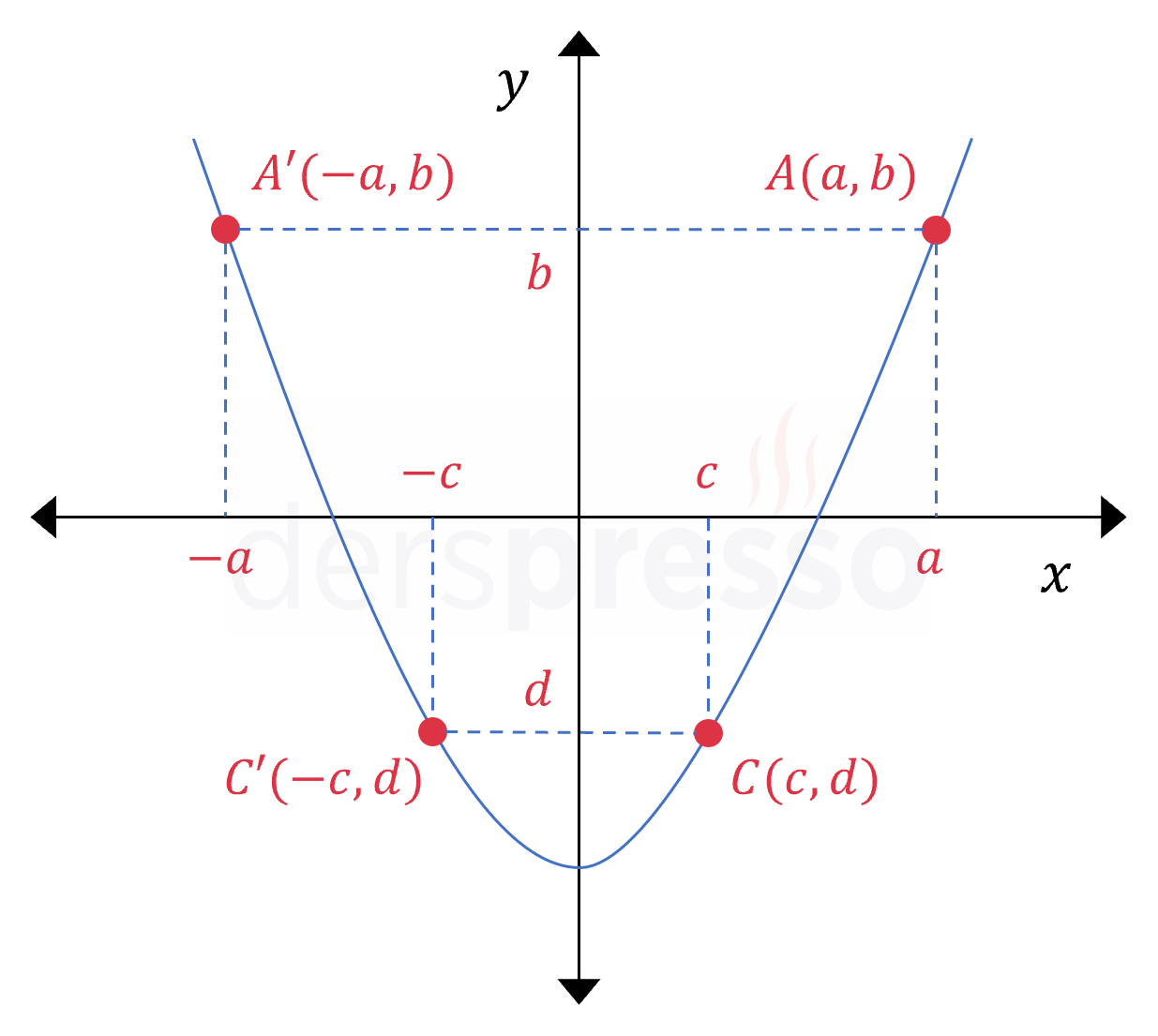
Tek ve Çift Fonksiyonlar
9.Sınıf Fonksiyonlar Konu Anlatımı Örnek Çözümlü Sorular Sunusu sunusunun Eşit Fonksiyon slaytını görüntülemektesiniz. EN ÇOK BAKILAN 9.Sınıf Fonksiyonlar Çözümlü Sorular ise f ve g fonksiyonlarına eşit fonksiyonlar denir. Eşit fonksiyonlar f = g biçiminde gösterilir. ÖRNEK A = {-2, 0, 2} ve B = {-8, 0, 8} kümeleri için, 3f : A ® B, f(x) = x ve g : A ® B, g(x) = 4x fonksiyonlarının eşit olup olmadığını bulalım. Sabit ve Sıfır Fonksiyonu f : A ® B, f(x) = c sabit fonksiyondur. (c Î R) f(x) fonksiyonu çift fonksiyondur. Eşit Fonksiyonlar. Tanım ve görüntü kümeleri birbiriyle aynı olan, tanım kümesindeki her bir elemanı için bu elemanların görüntüleri de aynı olan fonksiyonlara eşit fonksiyonlar denir. Periyodik Fonksiyon çözüm: Sıralı ikililerin eşit olmaları için, aynı sıradaki terimler eşit olmalı idi. Buradan,. fonksiyonuna "birebir ve örten fonksiyon" denir. Örnek: A f B 2 . .* 3 . .9 + . .12 a . .7 Birebir Örten Fonksiyon 6)Birebir İçine Fonksiyon: A'dan B'ye bir f fonksiyonunda A'nın farklı elemanlarının görüntüleri.
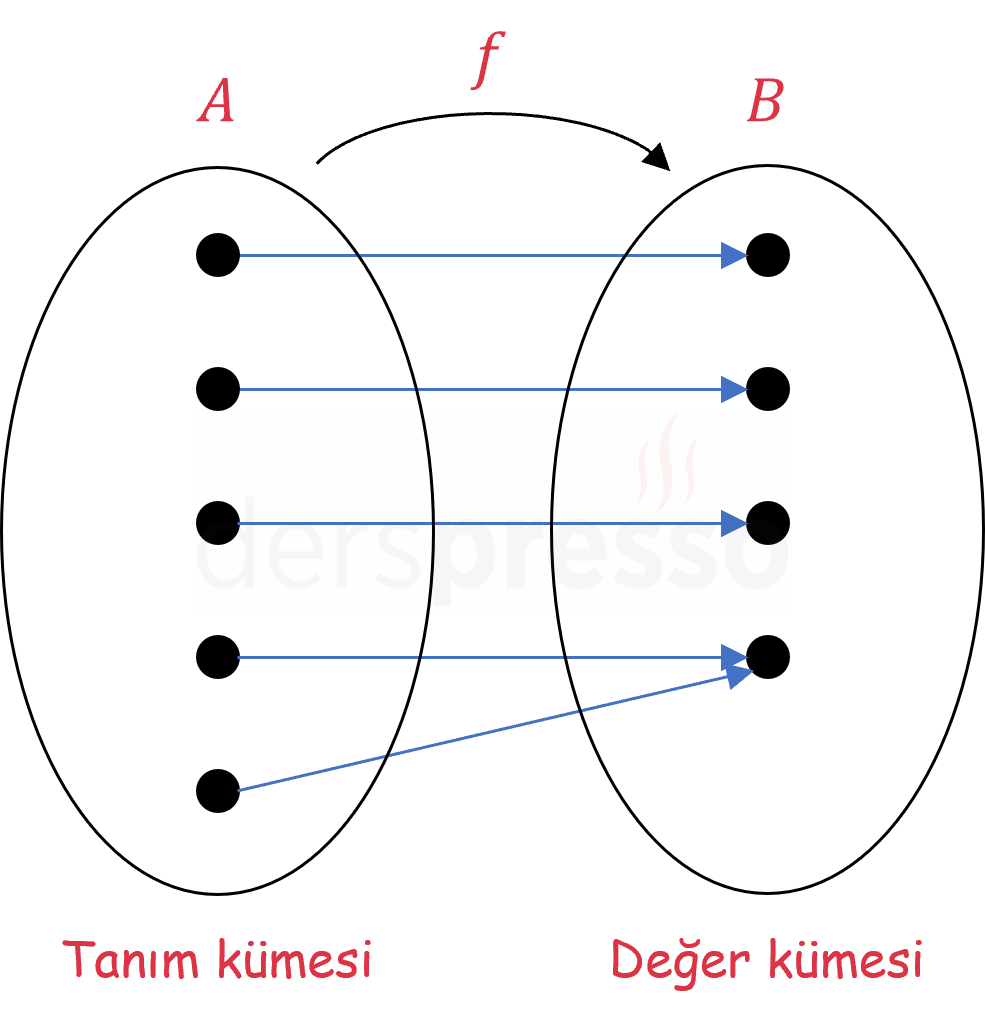
Örten ve İçine Fonksiyon
Parçalı fonksiyon, matematikte tanım aralığı alt aralıklara parçalanan ve her bir alt aralık için farklı bir fonksiyon olarak tanımlanan bir fonksiyon türüdür. Doğrusal (Lineer) Fonksiyon. a, b reel sayı olmak üzere, f : R → R, f(x) = ax + b şeklindeki fonksiyonlara doğrusal fonksiyon denir. Fonksiyon Olma Koşulları Diğer bir deyişle f A'dan B'ye fonksiyonunda a, b elemanı a için a ve b birbirinden farklı iken f (a) f (b) birbirinden farklı oluyorsa ya da f (a) f (b) birbirine eşit iken a b birbirine eşit oluyorsa f fonksiyonuna birebir fonksiyon denir. Verilen örnekte A'dan B'ye bir f fonksiyonu tanımlanmış. Fonksiyonun içi ve dışı aynı olan birbirine eşit olan fonksiyonlara birim fonksiyon diyorduk. Yani f(x)=x. Buna göre 3x-2=(a+2)x+b-3 oluyor. Yani a+2=3 b-3=-2 oluyor. Buradan da a=1 b=1 oluyor. Kaydırma (Ötelenme) Özelliği. L {t}'nin Laplace Dönüşümü. t^n: L {t^n}'nin Laplace Dönüşümü. Birim Adım Fonksiyonunun Laplace Dönüşümü. Ters Laplace Dönüşümü Örnekleri. Dirac Delta Fonksiyonu. Dirac Delta Fonksiyonunun Laplace Dönüşümü. Matematik >. Diferansiyel Denklemler >.

örten fonksiyon nedir
İki sayının çarpımının görüntüsü, sayıların ayrı ayrı görüntülerinin toplamına eşit ise bu fonksiyon bir logaritma fonksiyonudur. \( f(x) \ne 0, \quad x, y \gt 0 \) olmak üzere, \( f(x \cdot y) = f(x) + f(y) \) ise, Örnek. f: R→R, f fonksiyonu bir sabit fonksiyon olmak üzere f(x)= eşitliği veriliyor. Buna göre m nin değerini bulunuz.
Fonksiyon, matematikte değişken sayıları girdi olarak kabul edip bunlardan bir çıktı sayısı oluşmasını sağlayan kurallardır. Fonksiyon, 17. yüzyılda matematiğin kavramlarından biri olmuştur. Fizik, mühendislik, mimarlık ve birçok alanda kullanılmaktadır. Galile, Kepler ve Newton hareketlerin araştırılmasında, zaman ve mesafe arasındaki durumu incelemek için. Eksi 2'ye eşit olamasaydı, eksi 2'den büyük olmasını isteseydim, normal parantez işaretini kullanacaktık. Evet, eksi 2'ye eşit olabileceği için köşeli parantez. Aralığın diğer ucunda da, 98'e eşit olabileceği için yine köşeli parantezi seçeceğiz.
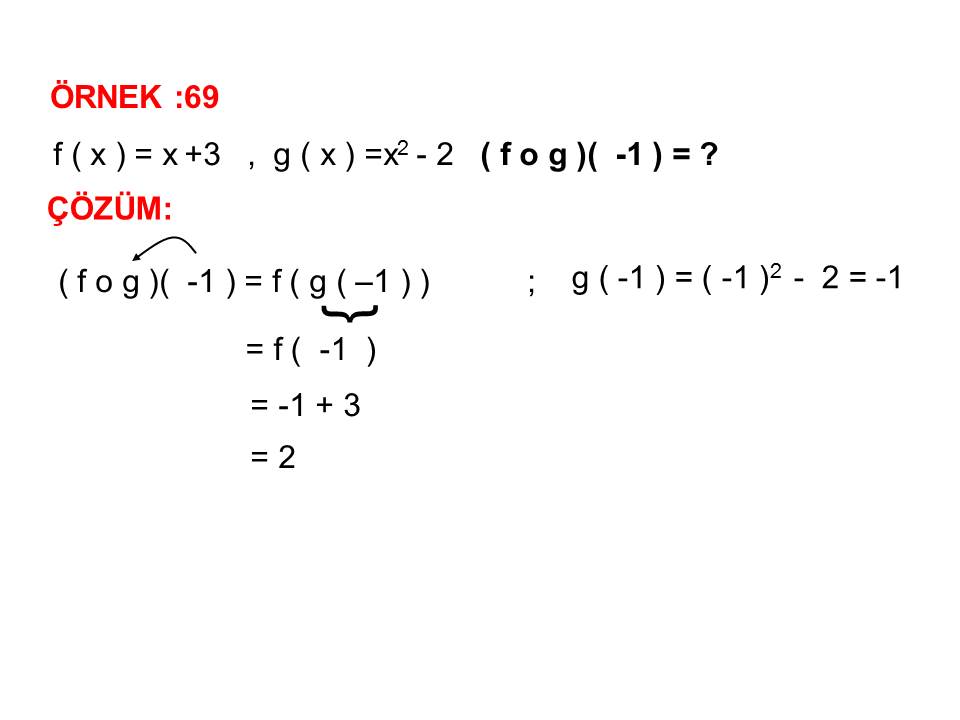
Bileşke Fonksiyonun Özellikleri →
Sadece y'yi x ile yeniden isimlendirdiğimi gösteriyorum. Gerçekten ne isim koymak isterseniz koyun yinede x eksi 1'in karaköküne eşit olacak. eksi 2 için x 1'e eşit yada 1'den büyük olacak. Ve şimdi x'in ters fonksiyonu var. Grafik haline getirecek olursak, elimden gelenin en iyisini yapacağım yine her zaman ki gibi. Ters Fonksiyon Kavramı. Bir fonksiyonun tersi f A'dan B'ye eşittir f x birebir ve örten bir fonksiyon olsun. Bu durumda Y eşittir f x fonksiyonun tersi f'in tersi b'den A'ya x eşittir f'in tersi y'dir. Yani bir fonksiyonun tersinden bahsedebilmemiz için birebir ve örten olması gerekiyor.