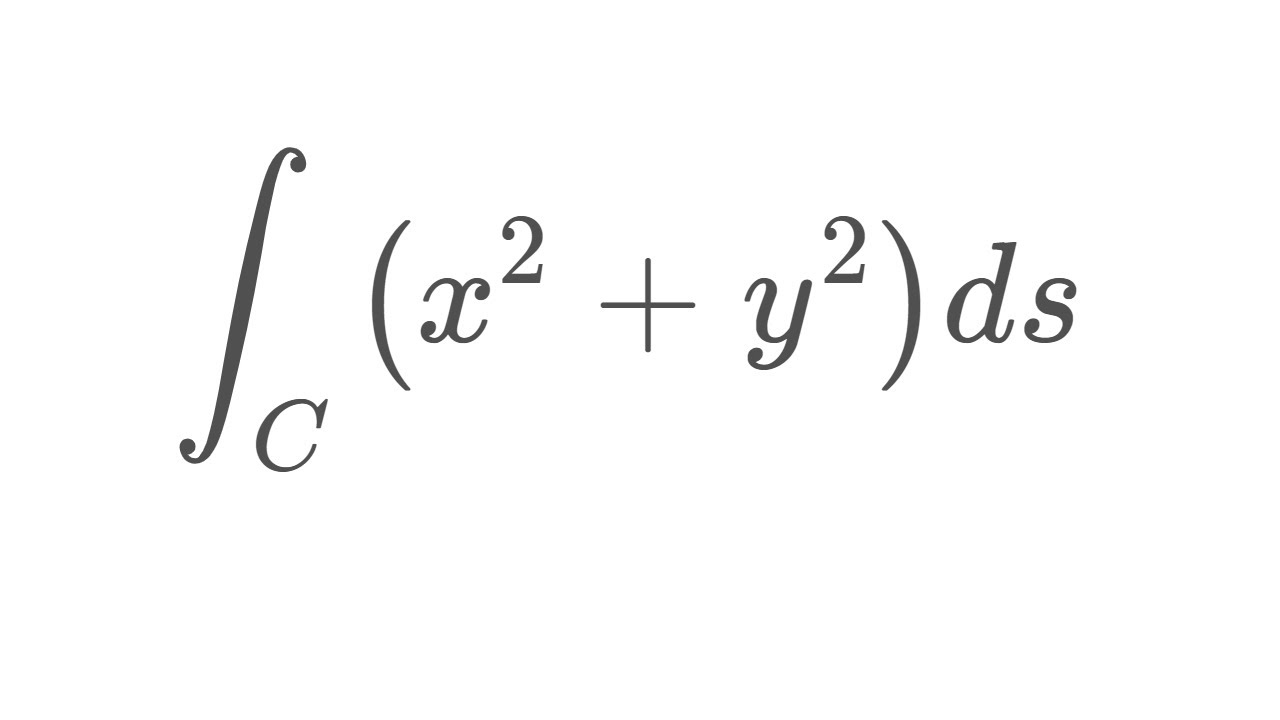This is the first video of a month-long series on vector calculus! In this video, I calculate the line integral of a function f with respect to s over a curv. The siege of İnegöl took place between Agios Nikolaos, the governor of the fort, and the Kayı army under the command of Turgut Bey. This conquest was one of the first conquests in Ottoman history after the siege of Kulaca Hisar. After the end of the siege, Tekfur Nikolaos was executed by Turgut Alp. [1] The conquest took place in 1299.

Line Koltuk Takımı 3+3+1inegöl mobilya
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.. The function to be integrated may be a scalar field or a vector field. That's essentially what we're doing. We're taking an integral over a curve, or over a line, as opposed to just an interval on the x-axis. We've taken the strange line integral, that's in terms of the arc length of the line, and x's and y's, and we've put everything in terms of t. Answer based on comments by Teddy. A line integral of the 1st kind, is the integral of a scalar ($\mathbb{R}^2 \to \mathbb{R}$, say) function, such as the one used in your question to calculate the area of a fence. Line integrals with triangle vertices. Evaluate the work integral where F(x, y) = −y, x over a triangle with vertices A(−2, −2), B(2, −2), C(0, 1). I am not sure how to approach this problem. I tried setting AB(4, 0), BC(−2, 3) and CA(−2, −3) but I am not sure how to proceed. for t ∈ [0, 1].

Inegöl Köfte First Orient Food
İnegöl (known as Ἀγγελόκωμις, Angelokomis in the Byzantine period) is a municipality and district of Bursa Province, Turkey. Its area is 1,118 km 2, and its population is 294,485 (2022). İnegöl is one of the centers of the Turkish furniture industry, and is also known for its meatball (İnegöl köftesi) which has its origins in ćevapi brought to the region by Bosnian. DEFINITION: Scalar Line Integral. Let f be a function with a domain that includes the smooth curve C that is parameterized by ⇀ r(t) = x(t), y(t), z(t) , a ≤ t ≤ b. The scalar line integral of f along C is. if this limit exists ( t ∗ i and Δsi are defined as in the previous paragraphs). Learning Objectives. 6.2.1 Calculate a scalar line integral along a curve.; 6.2.2 Calculate a vector line integral along an oriented curve in space.; 6.2.3 Use a line integral to compute the work done in moving an object along a curve in a vector field.; 6.2.4 Describe the flux and circulation of a vector field. Figure 16.7.1: Stokes' theorem relates the flux integral over the surface to a line integral around the boundary of the surface. Note that the orientation of the curve is positive. Suppose surface S is a flat region in the xy -plane with upward orientation. Then the unit normal vector is ⇀ k and surface integral.
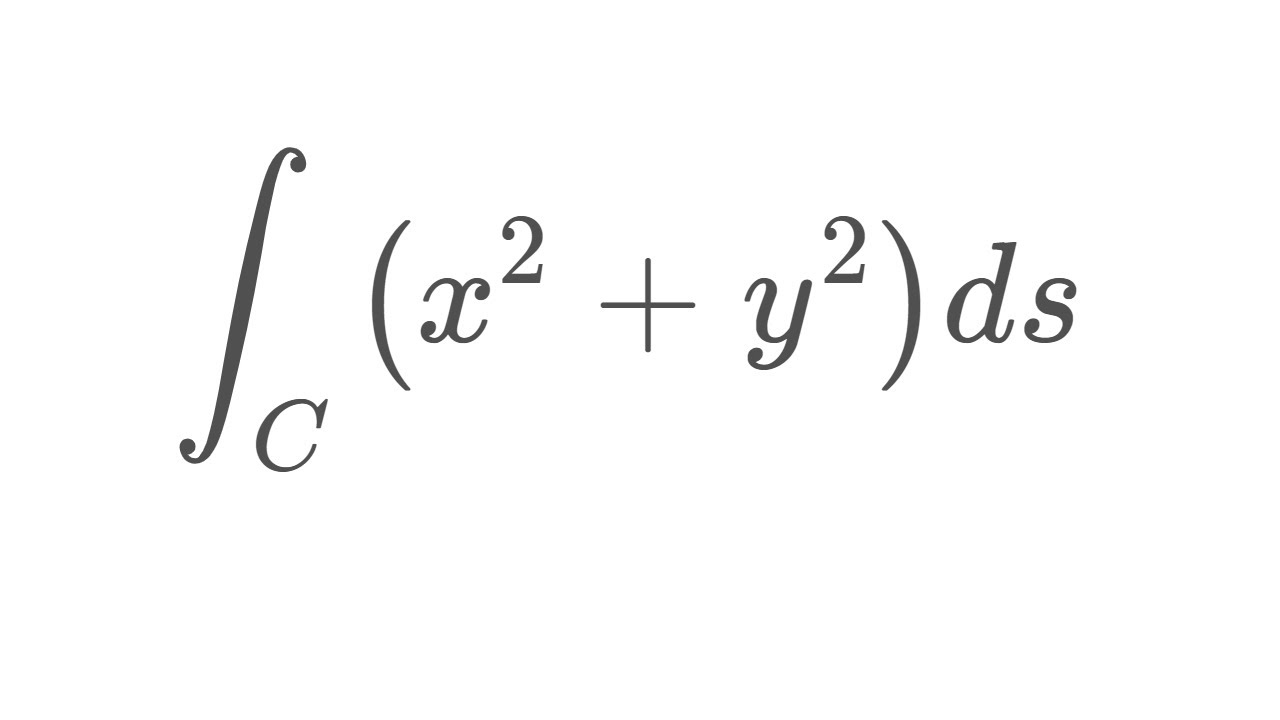
Integral
We are now ready to state the theorem that shows us how to compute a line integral. Theorem: Line Integrals of Vector Valued Functions. Let. r(t) = x(t)ˆi + y(t)ˆj a ≤ t ≤ b. be a differentiable vector valued function that defines a smooth curve C. Then. ∫C f(x, y) ds = ∫b af(x(t), y(t))√(x ′ (t))2 + (y ′ (t))2 dt. As we add up all the fluxes over all the squares approximating surface S, line integrals ∫ E l F · d r ∫ E l F · d r and ∫ F r F · d r ∫ F r F · d r cancel each other out. The same goes for the line integrals over the other three sides of E.These three line integrals cancel out with the line integral of the lower side of the square above E, the line integral over the left side of.
Section 16.3 : Line Integrals - Part II. In the previous section we looked at line integrals with respect to arc length. In this section we want to look at line integrals with respect to x x and/or y y. As with the last section we will start with a two-dimensional curve C C with parameterization, x = x(t) y = y(t) a ≤ t ≤ b x = x ( t) y = y. This video evaluates a line integral along a straight line segment using a parametric representation of the curve (using a vector representation of the line segment) and then integrating. A vector representation of a line that starts at r0 and ends at r1 is r (t) = (1-t)r0 + tr1 where t is greater than equal to 0 and lesser than equal to 1.

Question Video Evaluating the Line Integral of a Function of Two
When working with a line integral in which the path satisfies the condition of Green's Theorem we will often denote the line integral as, ∮CP dx+Qdy or ∫↺ C P dx +Qdy ∮ C P d x + Q d y or ∫ ↺ C P d x + Q d y. Both of these notations do assume that C C satisfies the conditions of Green's Theorem so be careful in using them. The county of İnegöl contains an 80km segment of the Evliya Çelebi Way, which is part of the Via Eurasia in Turkey. The route was re-waymarked and signposted in 2016-7 and includes 5-6 days of trekking on footpaths, old roads and forestry tracks. The entire route is suitable for horse-riding and mountain-biking, with some short detours in.