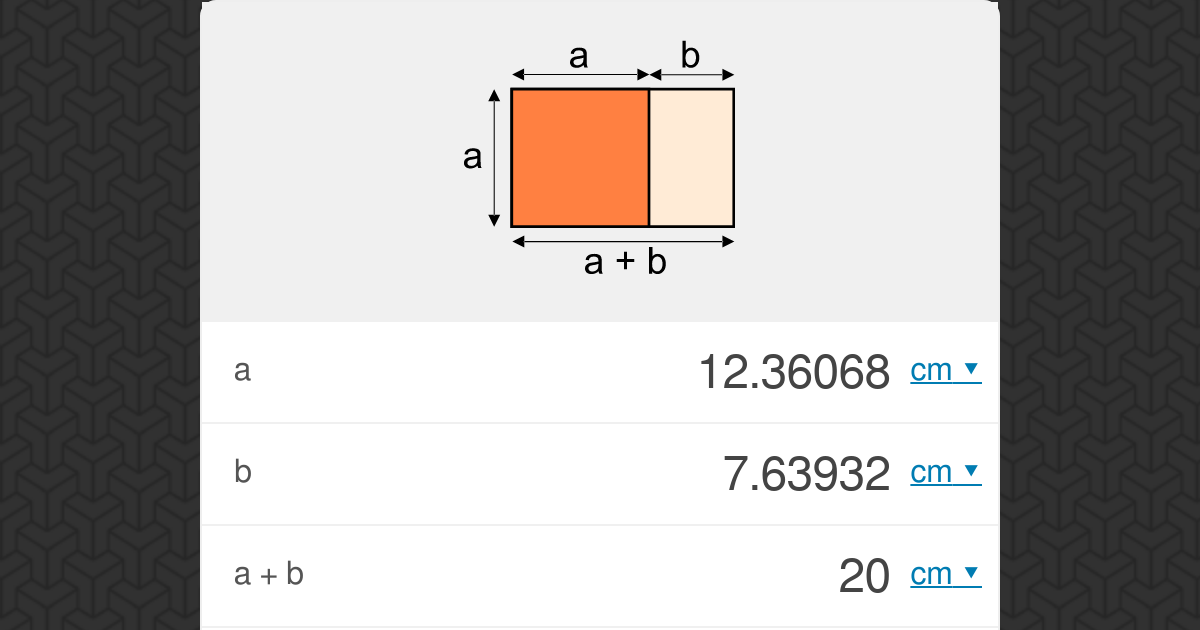
The golden rectangle is a rectangle whose sides are in the golden ratio, that is (a + b)/a = a/b = φ, where a is the width, a + b is the length of the rectangle, and φ is the golden ratio: φ = (1+√5)/2. The ratio calculator is an effective tool to assist in calculating ratios in general. The golden ratio calculator will calculate the length of the parts into which you need to divide a segment to obtain the golden ratio. Before we move on to actually computing the golden ratio, let's discuss what the golden ratio is all about. In what follows, you can find all the knowledge you need!
Golden Rectangle Calculator Omni
To calculate the area of the golden rectangle by hand, simply take the width "a" and multiply by the length "a + b". A = a (a + b) The calculator will quickly check your work for you. What if the scenario gives you the area but you need to calculate a side? Suppose you know a + b but not a? The Golden Rectangle Calculator is used to calculate the golden rectangle based on the length of a single side. Golden Rectangle In geometry, a golden rectangle is one whose side lengths are in the golden ratio (approximately 1:1.618). Outer and Interior Golden Rectangle Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Written as φ, the Greek letter phi, the Golden Ratio is an irrational value that can be found by cutting a line into two sections whereby the longer section A divided by the shorter section B is equivalent to A+B (the full length of the line) divided by A. As an equation, the Golden Ratio is written as: A/B = (A+B)/A = 1.6180339887498948420.
Caiet Persoana responsabilă cu jocul sportiv Grozav golden number calculator Gimnastică
Golden Ratio Calculator • Enter just one number to create a golden ratio or, • Enter both A and B for comparison or, • Enter both A+B and A for comparision A+B : A = A : B : = : Round to Decimal Places Answer: A = 7.416 B = 4.583 A+B = 12 A/B = 1.618 (A+B)/A = 1.618 PHI = 1.618 A + B : A = A : B 12 : A golden rectangle is a rectangle whos ratio of length to width is equal to the golden ratio of 1.6180399. Enter either the length or width of a golden rectangle into the calculator to determine the missing side length. The Golden Ratio is equal to: 1.61803398874989484820. (etc.) The digits just keep on going, with no pattern. In fact the Golden Ratio is known to be an Irrational Number, and I will tell you more about it later. Formula We saw above that the Golden Ratio has this property: a b = a + b a Given a rectangle having sides in the ratio 1:phi, the golden ratio phi is defined such that partitioning the original rectangle into a square and new rectangle results in a new rectangle having sides with a ratio 1:phi. Such a rectangle is called a golden rectangle. Euclid used the following construction to construct them. Draw the square square ABDC, call E the midpoint of AC, so that AE=EC.

Proporción Aurea Fibonacci Golden Ratio, Fibonacci Spiral, The Golden Mean, Golden Rule
An online golden ratio calculator is programmed to determine golden ratio value by using either small side, longer side or the sum of two. But wait! Before you move on, let us tell you that you must go through the basic idea of golden ratio. Let's dive in! What Is The Golden Ratio? In geometrical analysis: Using the golden ratio equation, you get the value: ɸ = 1 + √ 5 2. ɸ = 1.6180339887. Or. ɸ = 1.62. The golden ratio is also known as the mean ratio, extreme ratio, medial section, Sectio Divina (divine section), golden number, golden cut, golden proportion, and divine proportion. In layman terms, we can exemplify the golden ratio as a line.
A golden rectangle is a rectangle whose ratio of the two sides a and b is the golden ratio. The golden ratio is defined by (a + b): a = a: b, it is approximately 1.62. The online calculator calculates the side lengths a and b, the diagonal, the circumference and the area for a golden rectangle. One of the values must be known. A golden rectangle, in geometry, is a rectangle whose sides are in the golden ratio. In math, two random quantities are in the golden ratio if their ratio is the same as is the ratio of their sum to the larger of those two quantities. Algebraically speaking, for a and b quantities with a>b>0 , \frac {a+b} {a} = \frac {a} {b} = \varphi
Golden Ratio Calculator With Solution FAEDHI
Step 2: Find the shorter part and name it with the letter b. Step 3: Fill in the blanks in the formula. Step 4: Divide the sum of a and b by a. Step 5: Take a and divide it by b. Step 6: The golden ratio equals around 1.618 if the proportion is in the golden ratio. Step 7: To double-check your answer, use the golden ratio calculator. A golden rectangle is a rectangle whose length to width ratio equal to the golden ratio, φ, which has a value of or approximately 1.618, assuming the length is the larger value. The following diagram shows what it looks like visually: Golden rectangles have been used throughout history in architecture, art, and other areas, both intentionally.




