How to construct (draw) a regular pentagon inscribed in a circle. The largest pentagon that will fit in the circle, with each vertex touching the circle.. Regular pentagon inscribed in a circle. Printable step-by-step instructions. The above animation is available as a printable step-by-step instruction sheet, which can be used for making. 0:00 / 5:33 How to draw a regular pentagon inscribed in a circle Arthur Geometry 83.2K subscribers Subscribe Subscribed 7.1K 795K views 7 years ago 2nd - 3rd ESO - Visual Arts - Geometry How.
You won't Believe This.. 14+ Little Known Truths on Irregular Pentagon Shape Images? Find the
Area A of a regular pentagon can be calculated from the formula: area = a² × √ (25 + 10√5) / 4, where a is a side of a regular pentagon. Also, you can find the area having the circumscribed circle radius: area = 5R² × √ [ (5 + √5)/2] / 4, where R is the circumcircle radius. Regular pentagons Side ( ), circumradius ( ), inscribed circle radius ( ), height ( ), width/diagonal ( ) A regular pentagon has Schläfli symbol {5} and interior angles of 108°. A regular pentagon has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). Draw a broad arc that crosses the given circle in two places. Label them A and E. 9. Set the compasses on M and adjust its width to N. 10. Draw a broad arc that crosses the given circle in two places. Label them B and D. 11. Draw a line from A to B, then B to C etc, until you have drawn all five sides of the pentagon. How to construct a regular pentagon inside a circle using compass and ruler. In this tutorial we will learn how to draw a regular pentagon step by step.
Pentagon Inscribed & Circumscribed in Circles ClipArt ETC
1. Initiate with a Circle: Begin by drawing a circle of the desired radius using the compass. 2. Determine the Central Angle: The central angle is crucial and is given by the formula: Central Angle \ (= \frac {360^\circ} {n}\) Where \ (n\) is the number of sides of the regular polygon. 3. Constructing Polygon Vertices: - Definitions - Properties of regular pentagons - Symmetry - Interior angle and central angle - Circumcircle and incircle - Area and perimeter - Bounding box - How to draw a regular pentagon - Examples - Regular pentagon cheat-sheet - See also Definitions Pentagon is a polygon with five sides and five vertices. The regular pentagon is the regular polygon with five sides, as illustrated above. A number of distance relationships between vertices of the regular pentagon can be derived by similar triangles in the above left figure, (1) where is the diagonal distance. A regular pentagon is a five-sided polygon with sides of equal length and interior angles of 108° (3π/5 rad). Because 5 is a Fermat prime, you can construct a regular pentagon using only a straightedge and compass. Steps Download Article 1 Draw a line segment AB. [1] 2 Draw two circles, 1 and 2, centred at A and B, both with radius AB.

Approximate regular pentagon from the given inscribed circle Download Scientific Diagram
Regular Polygon in a Circle Author: AMW0ng, David Griswold Topic: Circle Enter a number of sides (from 3 to 360), use the slider, or use the next and prev buttons to inscribe a regular polygon in the circle of radius 7 provided. The Apothem (the dashed line in the applet below) is the length from the center of the regular to one of its sides. Inscribing a regular pentagon in a circle - and proving it Scott E. Brodie Constructions by straight-edge and compass of several regular polygons - the equilateral triangle, square, hexagon, and octagon, are familiar. Indeed, the construction of an equilateral triangle is the very first proposition in Euclid's Elements (I.1).
This video shows how to draw a regular pentagon inscribed in a circle.#Pentagoninscribedinacircle #polygonsHello Teachers! For you to be updated for more lea. Draw pentagon with compass.How to Draw a pentagon inscribed in a given circle. Step-by-step Super easy!
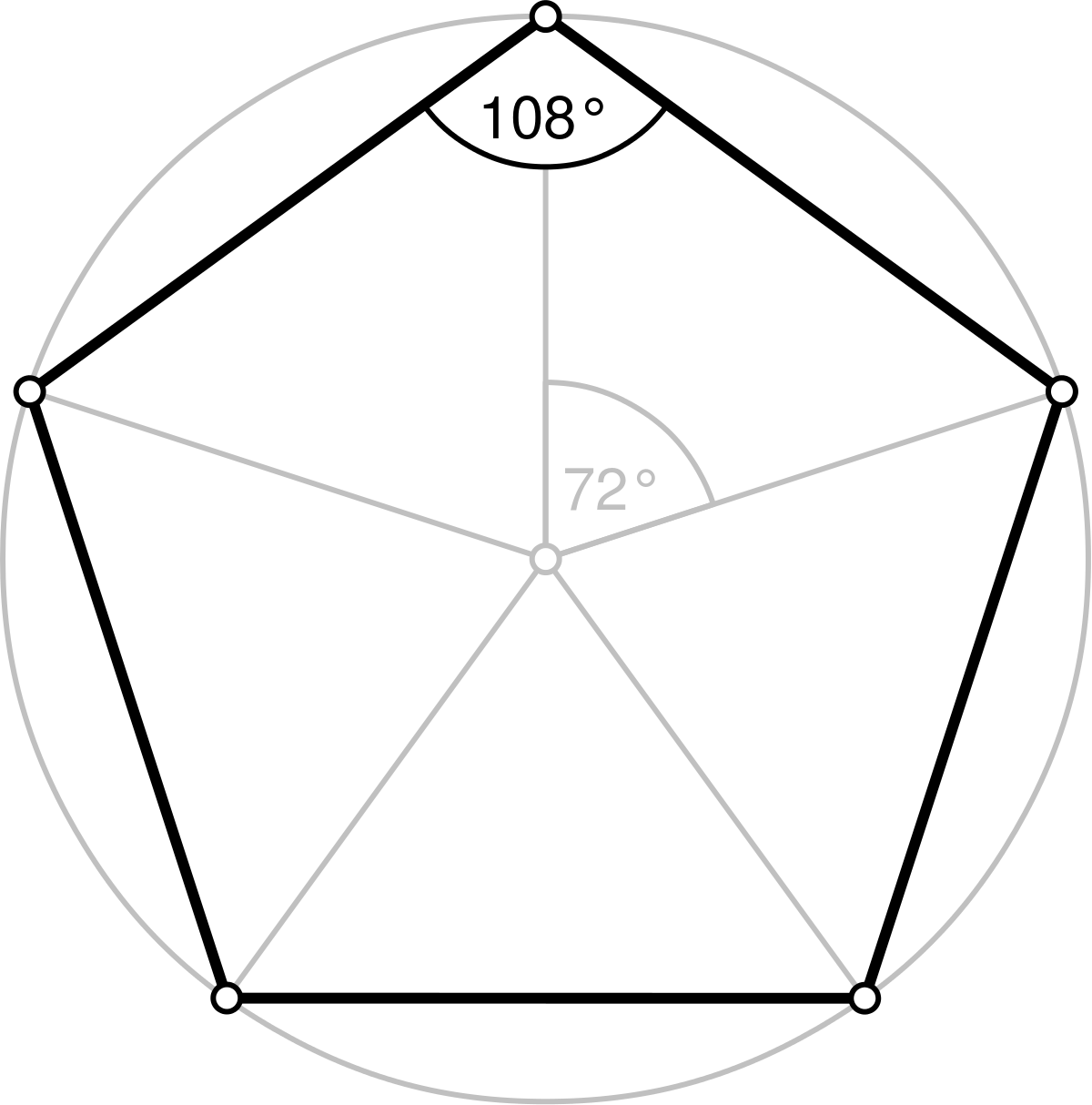
Pentagon Wikipedia
In this video, I'll show you how to construct a regular pentagon given the diameter of the circumscribing circle. To inscribe a regular pentagon in a circle, first draw perpendicular radii OA and OB from the center O of a circle. Let C be the midpoint of OB and draw AC. Bisect angle ACO to meet OA at D. Draw a perpendicular DE to OA to the circle. Then AE is one side of the pentagon. The remaining sides can then be constructed.



