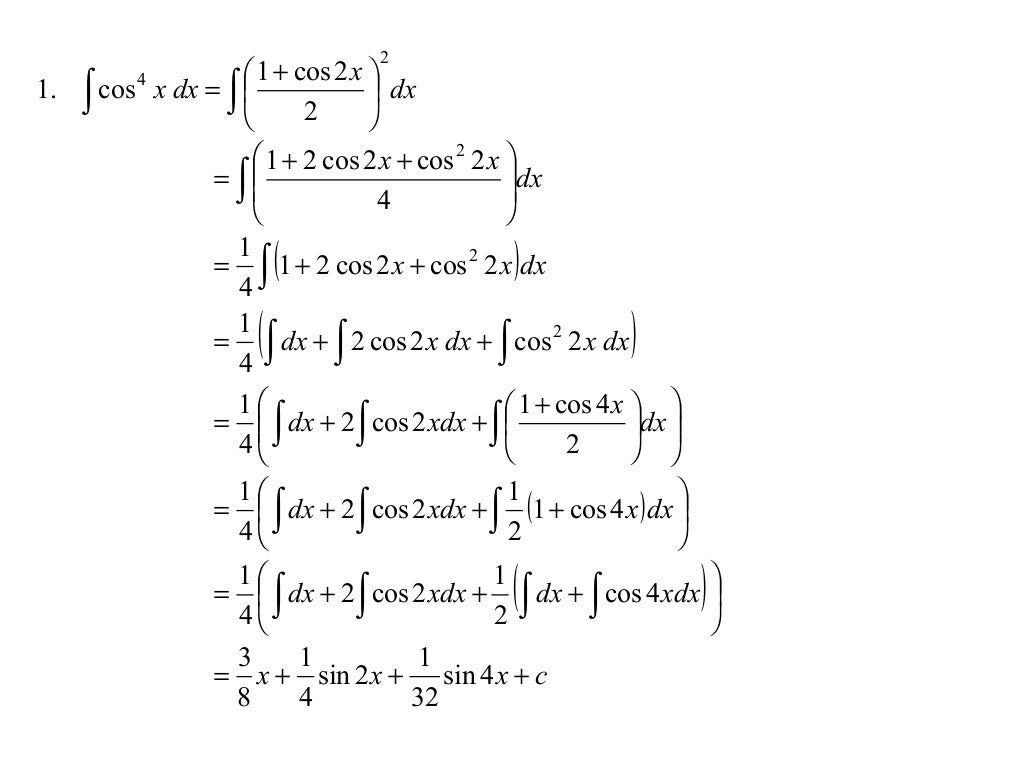Aşağıdaki liste trigonometrik fonksiyonların integrallerini içermektedir. İntegral fonksiyonlarının tüm bir listesi için lütfen İntegral tablosu sayfasına bakınız. c sabiti sıfırdan farklı varsayılmıştır. Sadece Sinüs içeren trigonometrik fonksiyonların integralleri c burada integral sabitidir: Not: cvs {x} fonksiyonu 1-sinx'e eşittir. Aşağıdaki formdaki trigonometrik fonksiyonların integrali trigonometrik özdeşlikler ve değişken değiştirme yöntemi yardımıyla alınabilir. olmak üzere, Bu ifadelerin integralini almak için kullanılacak yöntem üslerin tek ve çift olmasına göre aşağıdaki gibidir. ÖRNEK 1: ifadesinin integralini bulalım. Verilen ifadede sinüsün üssü tek sayıdır.

Contoh Soal dan Pembahasan Integral Trigonometri Berpangkat
Unsourced material may be challenged and removed. The following is a list of integrals ( antiderivative functions) of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antiderivative functions, see Lists of integrals. integralinde seçilir. Buradan; elde edilir. Kısmi integralde u yu seçerken LAPTÜ yöntemini kullanabiliriz. Yani sırasıyla aşağıdaki fonksiyonlardan ilk gördüğümüz diğeri olarak alınır. Logaritmik fonksiyon Arc (ters trigonometrik fonksiyonlar) Polinom fonksiyon Trigonometrik fonksiyon üstel fonksiyon Rasyonel Fonksiyonların İntegrali Trigonometri İntegral; Trigonometrik fonksiyonların belirli integralleri vardır. Öncelikle trigonometrik fonksiyonları hatırlamakta fayda var. Trigonometrik fonksiyonlar; Sinüs = sin = karşı dik kenar uzunluğu / hipotenüs uzunluğu Cosinüs = Cos = komşu dik kenar uzunluğu / hipotenüs uzunluğu BUders üniversite matematiği derslerinden calculus-I dersine ait "Trigonometrik Dönüşüm Yardımıyla İntegral Alma (1. Bölüm)" videosudur. Hazırlayan: Kemal Duran (Matematik Öğretmeni).

INTEGRAL SUBSTITUSI TRIGONOMETRI EPUB DOWNLOAD
Kısmi İntegral Kullanarak x²⋅𝑒ˣ 'in İntegralini Hesaplama (Bir ekran açılır) Kısmi İntegral Kullanarak 𝑒ˣ.cos(x) 'in İntegralini Hesaplama. Trigonometri ve U-Dönüşümü (2. Bölüm) (Bir ekran açılır) Tanjant İle Trigonometrik Yerine Koyma Sin x. Cosec x=1 Cos xSec x=1 Tümler Açı ve Trigonometri Formülleri Cos (π/2-x)=Sin x ve Sin (π/2-x)=Cos x Cot (π/2-x)=Tan x ve Tan (π/2-x)=Cot x Cosec (π/2-x)=Secx ve Sec (π/2-x)=Cosec x Tümler Açı Özellikleri (Radyan Cinsinden) Cos (90-x)=Sinx ve Sin (90-x)=Cos x Cot (90-x)=Tanx ve Tan (90-x)=Cot x Sec (90-x)=Cosecx ve Cosec (90-x)=Sec x Exercise 7.2.2. Evaluate ∫cos3xsin2xdx. Hint. Answer. In the next example, we see the strategy that must be applied when there are only even powers of sinx and cosx. For integrals of this type, the identities. sin2x = 1 2 − 1 2cos(2x) = 1 − cos(2x) 2. and. cos2x = 1 2 + 1 2cos(2x) = 1 + cos(2x) 2. Bilimsel ve Teknik Yayınları Çeviri Vakfı tarafından Türkçeleştirilmektedir. ©2022 Khan Academy®. 11. Sınıf Matematik konusundaki Trigonometrik Formülleri Kullanma başlıklı ders videosuna buradan ulaşabilirsiniz. | Khan Academy Türkçe.
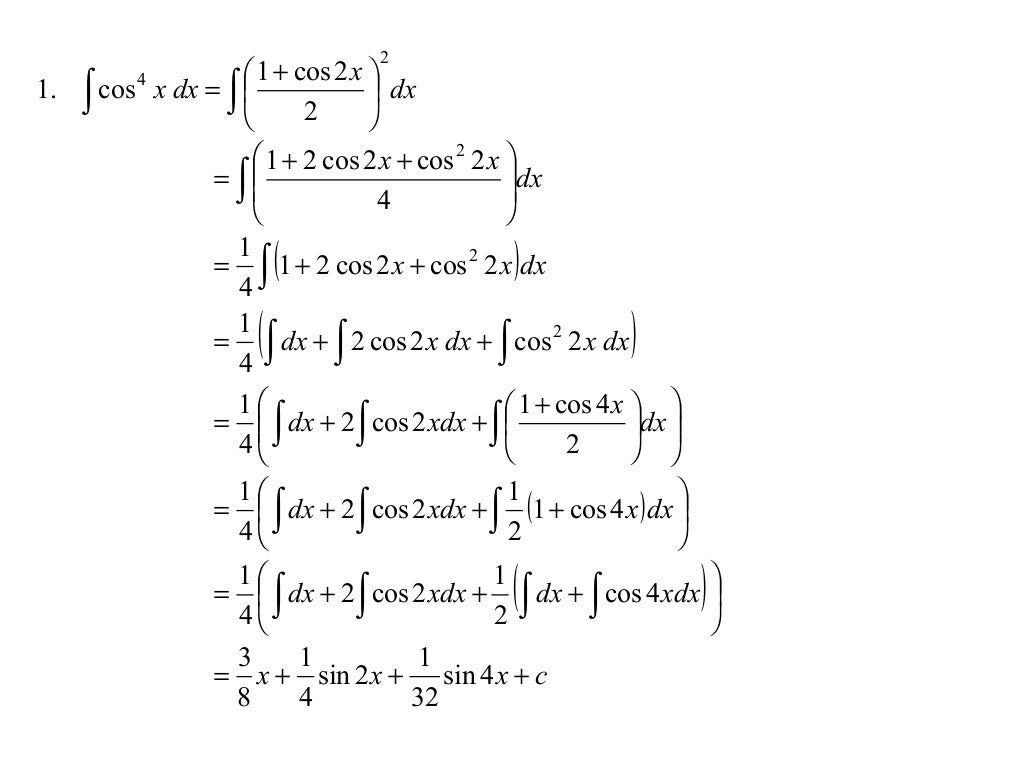
04 integral trigonometri
Bu formüller arasında en yaygın olanlar "belirli integral" ve "belirsiz integral"dir. Belirli integral, bir fonksiyonun bir belirli aralıkta toplam değerini bulurken, belirsiz integral, bir fonksiyonun bir değişken değiştirilerek çözülebilen integral formülünü bulmaya yarar. Bu sayfada Trigonometrik Üçgen Formülleri (Dik Üçgen Formülleri), Bölgelere Göre İşaret, Sinüs Teoremi, Sinüs Alan Formülü, Kosinüs Teoremi, Ters Trigonometrik Fonksiyonlar, Toplam Fark Formülleri, İki Kat Açı Formülleri, Yarım Açı Formülleri, Dönüşüm Formülleri, Ters Dönüşüm Formülleri ve Trigonometri Tablosuna ulaşabilirsiniz.
Trigonometri Ters Dönüşüm Formülleri; Trigonometri kapsamı ve içeriği bol olan bir konudur. Matematiğin doğrudan doğruya astronomiden çıkmış bir uzantıdır. Trigonemetri kavramı Babilliler ve Mısırlılar döneminden itibaren biliniyor.. Trigonometrik İntegral: Trigonometri İntegral; Trigonometrik fonksiyonların belirli. In this section we look at how to integrate a variety of products of trigonometric functions. As a collection, these integrals are called trigonometric integrals.They are an important part of the integration technique called trigonometric substitution, which is featured in Section 2.3: Trigonometric Substitution.This technique allows us to convert algebraic expressions that we may not be able.

Integral + Integral Trigonometri
Buna göre, α+β = 90° ise sinα = cosβ α+β = 90° ise tanα = cotβ α+β = 90° ise secα = cscβ sonucuna ulaşılır. Trigonometri Dönüşüm Formülleri Sinx+siny = 2. Sin [ (X+y)/2]. Toplam ve Fark formülleri : cos (A - B) = cosA cosB + sinA sinB cos (A + B) = cosA cosB - sinA sinB sin (A - B) = sinA cosB - cosA sinB sin (A + B) = sinA cosB + cosA sinB . Trigonometri formülleri 3 Yarım açı formülleri : sin 2x = 2 sinx .cosx cos 2x = cos 2 x - sin 2 x = 1 - 2 sin 2 x = 2 cos 2 x - 1. Yarım açı.