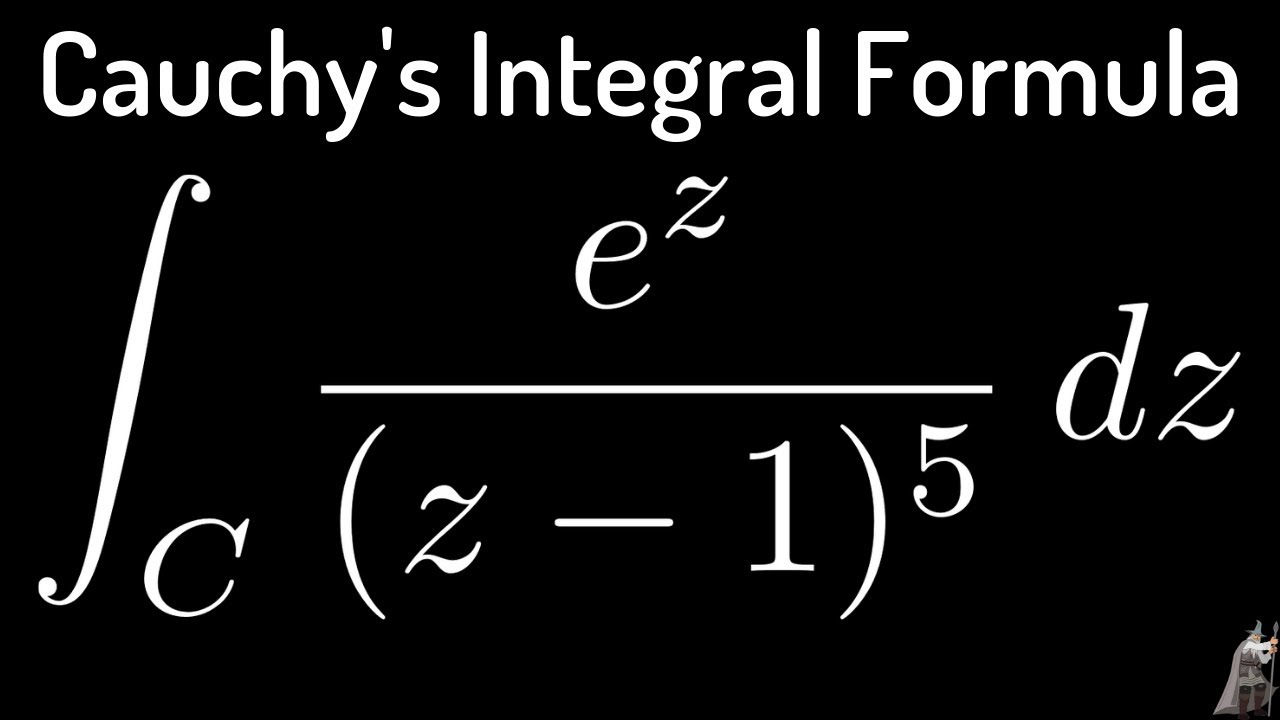In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. 4 Cauchy's integral formula 4.1 Introduction Cauchy's theorem is a big theorem which we will use almost daily from here on out. Right away it will reveal a number of interesting and useful properties of analytic functions. More will follow as the course progresses. If you learn just one theorem this week it should be Cauchy's integral.
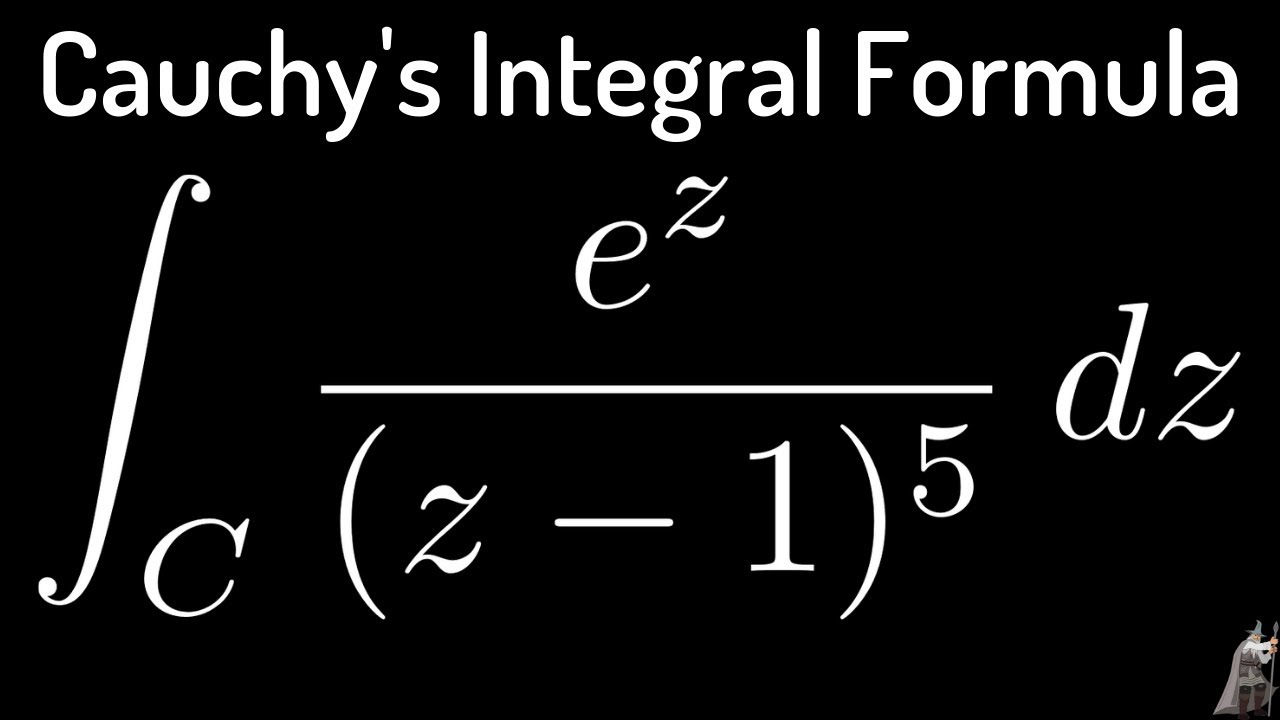
Cauchy's Integral Formula/Cauchy's Differentiation Formula used to Integrate e^z/(z 1)^5 YouTube
This page titled 5.2: Cauchy's Integral Formula for Derivatives is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Jeremy Orloff (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Cauchy's integral formula states that f(z_0)=1/(2pii)∮_gamma(f(z)dz)/(z-z_0), (1) where the integral is a contour integral along the contour gamma enclosing the point z_0. It can be derived by considering the contour integral ∮_gamma(f(z)dz)/(z-z_0), (2) defining a path gamma_r as an infinitesimal counterclockwise circle around the point z_0, and defining the path gamma_0 as an arbitrary. UniversityofToronto-MAT334H1-F-LEC0101 ComplexVariables 9-Cauchy'sIntegralFormula Jean-BaptisteCampesato October14th,2020 Contents 1 Simpleconnectedness 1 Proof of Cauchy's integral formula. We reiterate Cauchy's integral formula from Equation 5.2.1: f(z0) = 1 2πi ∫C f(z) z −z0 dz f ( z 0) = 1 2 π i ∫ C f ( z) z − z 0 d z. Proof P r o o f. (of Cauchy's integral formula) We use a trick that is useful enough to be worth remembering. Let.

Cauchy Integral Formula with Examples Complex Analysis by a Physicist YouTube
We may view Equation as a special instance of integrating a rational function around a curve that encircles all of the zeros of its denominator. In particular, recalling that Cauchy's Theorem, we find. ∫ q ( z) d z = ∑ j = 1 h ∑ k = 1 m j ∫ q j, k ( z − λ j) k d z = 2 π i ∑ j = 1 h q j, 1. To take a slightly more complicated. We assume C C is oriented counterclockwise. Figure 5.1.1 5.1. 1: Cauchy's integral formula: simple closed curve C C, f(z) f ( z) analytic on and inside C C. (CC BY-NC; Ümit Kaya) Then for any z0 z 0 inside C C: f(z0) = 1 2πi ∫C f(z) z −z0 dz f ( z 0) = 1 2 π i ∫ C f ( z) z − z 0 d z. This is remarkable: it says that knowing the. The Cauchy integral formula states that the values of a holomorphic function inside a disk are determined by the values of that function on the boundary of the disk. More precisely, suppose f: U \to \mathbb {C} f: U → C is holomorphic and \gamma γ is a circle contained in U U. Then for any a a in the disk bounded by \gamma γ, 18.04 S18 Topic 4: Cauchy's integral formula. Resource Type: Lecture Notes. pdf. 295 kB 18.04 S18 Topic 4: Cauchy's integral formula Download File DOWNLOAD. Course Info Instructor Dr. Jeremy Orloff; Departments Mathematics; As Taught In Spring 2018.

Cauchy integral formula in complex plane. Download Scientific Diagram
5.2: Cauchy's Integral Formula for Derivatives Cauchy's integral formula is worth repeating several times. So, now we give it for all derivatives f(n)(z) of f . This will include the formula for functions as a special case. 5.3: Proof of Cauchy's integral formula; 5.4: Proof of Cauchy's integral formula for derivatives Cauchy's integral formula is a central statement in complex analysis in mathematics. It expresses that a holomorphic function defined on a disk is determined entirely by its values on the disk boundary. For all derivatives of a holomorphic function, it provides integration formulas. Also, this formula is named after Augustin-Louis Cauchy.
In applications, the boundary is often only piecewise smooth, and again that is all we need for Stokes. Theorem 4.1. 1: Cauchy-Pompeiu. Let U ⊂ C be a bounded open set with piecewise- C 1 boundary ∂ U oriented positively (see appendix B ), and let f: U ¯ → C be continuous with bounded continuous partial derivatives in U. Cauchy's integral formula still holds in that case. The proof is left for the reader. Examples Let Cbe the unit circle centered in 0 and traversed in the counterclockwise direction. Z C cosz z dz= 2ˇin(C;0)cos(0) = 2ˇi Let be the arc composed of the line segment [ 2 p 3 ;2 p 3] along the real axis, and the upper half of

cauchy integral theorem Liberal Dictionary
Chapter & Page: 15-4 Cauchy Integral Theorems and Formulas and, thus, equation (15.2) reduces to I C f (z)dz = − ZZ S 0dA + i ZZ S 0dA = 0 . Since every closed curve can be decomposed into a bunch of simple closed curves, the above Physics 2400 Cauchy's integral theorem: examples Spring 2017 and consider the integral: J= I C [z(1 z)] 1 dz= 0; >1; (4)where the integration is over closed contour shown in Fig.1.