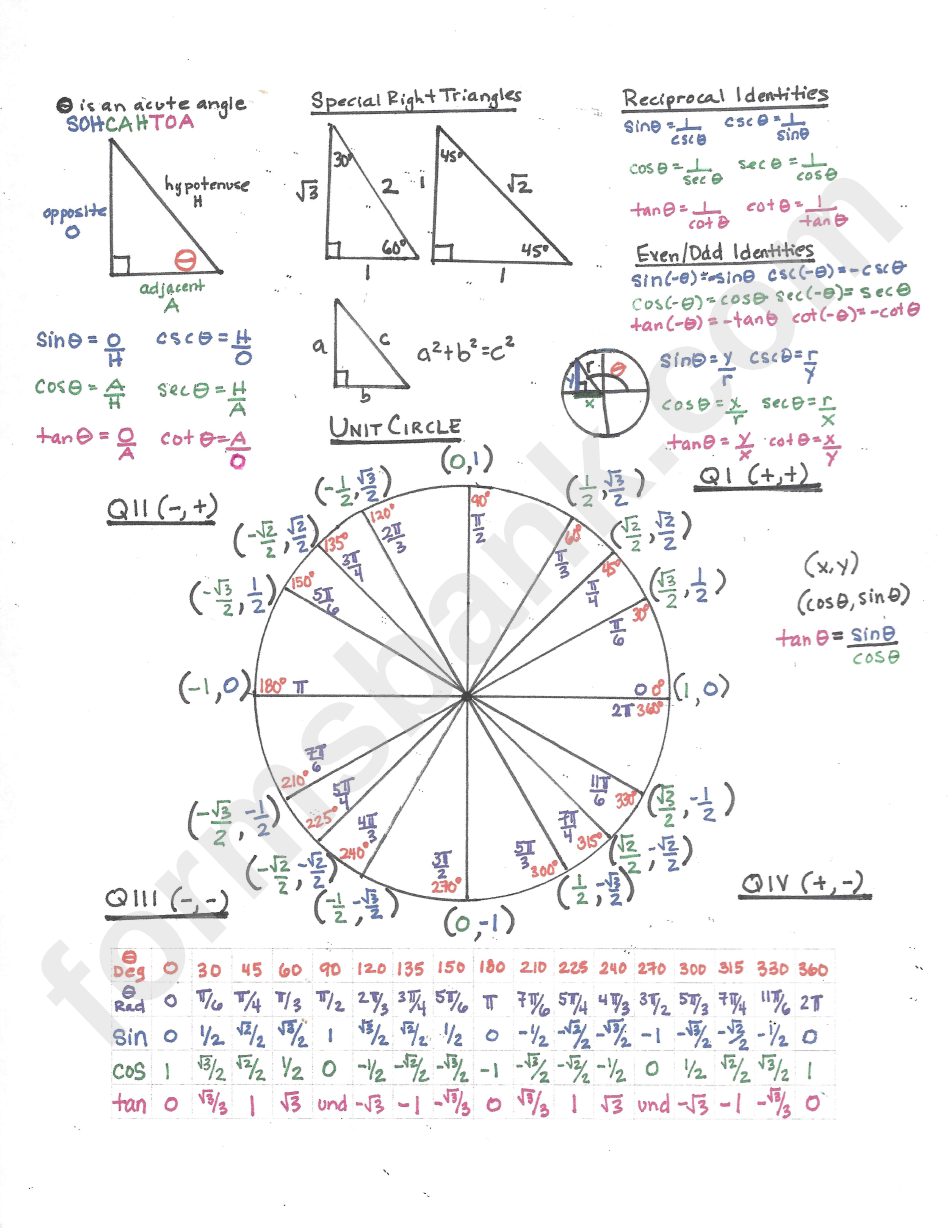
Trig_Cheat_Sheet Author: ptdaw Created Date: 11/2/2022 7:09:02 AM. Pythagorean Identities \cos^2 (x)+\sin^2 (x) = 1 \sec^2 (x)-\tan^2 (x) = 1 \csc^2 (x)-\cot^2 (x) = 1 Double-Angle Identities \sin (2x)=2\sin (x)\cos (x) \cos (2x)=1-2\sin^2 (x) \cos (2x) = 2\cos^2 (x)-1 \cos (2x) = \cos^2 (x)-\sin^2 (x) \tan (2x) = \frac {2\tan (x)} {1-\tan^2 (x)} Sum/Difference Identities

Trig_Cheat_Sheet.pdf Sine Trigonometric Functions
Symbolab Trigonometry Cheat Sheet Basic Identities: (tan )=sin(𝑥) cos(𝑥) (tan )= 1 cot(𝑥) (cot )= 1 tan(𝑥)) cot( )=cos(𝑥) sin(𝑥) sec( )= 1 cos(𝑥) USEFUL TRIGONOMETRIC IDENTITIES Unit circle properties cos(ˇ x) = cos(x) sin(ˇ x) = sin(x) tan(ˇ x) = tan(x) cos(ˇ+x) = cos(x) sin(ˇ+x) = sin(x) tan(ˇ+x) = tan(x) Trigonometric Identities Cheat Sheet Quotient Identities tan = sin cos cot = cos sin Reciprocal Identities sin = 1 csc cos = 1 sec tan = 1 cot Co-function Identities sin = cos 2 cos = sin 2 tan = cot 2 csc = sec 2 sec = csc 2 cot = tan 2 Phytagorean Identities sin2 cos2 = 1 1 tan2 = sec2 1 cot2 = csc2 Double Angle Identities Having a comprehensive cheat sheet can be immensely helpful in simplifying expressions, solving equations, and understanding the properties of trigonometric functions. Below are some essential trigonometric identities: 1. Pythagorean Identities: Sin²θ + Cos²θ = 1 1 + Tan²θ = Sec²θ 1 + Cot²θ = Csc²θ 2.
Basics Cheat Sheet Html basics cheat sheet by katie Tutorial Blog
Trig Reciprocal Identities, trigonometry is a branch of mathematics that studies the relationships between angles and lengths in triangles. Trigonometry Ratios with Formulas Ready to discover the fundamental building blocks of Trigonometry? Trigonometry Ratios can help you do just that! Sum and Difference Trig Identities Free Download of Trig Identities Cheat Sheet (PDF) Trig Identities Formula Sheet (PDF) (2880 downloads) Published: March 2, 2019 - Last updated: November 22, 2022 I created this free printable trig identities cheat sheet for my Pre-Calculus students to reference as we work through our unit on trigonometric identities. TrigCheatSheet DefinitionoftheTrigFunctions Righttriangledefinition Forthisdefinitionweassumethat 0 < < ˇ 2 or0 < < 90 . sin( ) = opposite hypotenuse csc( ) = hypotenuse 7 years ago. The easiest way is to see that cos 2φ = cos²φ - sin²φ = 2 cos²φ - 1 or 1 - 2sin²φ by the cosine double angle formula and the Pythagorean identity. Now substitute 2φ = θ into those last two equations and solve for sin θ/2 and cos θ/2.

Trig cheat sheet daxsnap
Formulas and Identities Definition of the Trig Functions Right triangle definition For this definition we assume that 0 < θ < π or 0 ° < θ < 90 ° . 2 hypotenuse opposite θ adjacent Unit circle definition For this definition θ is any angle. y ( x , y ) y 1 θ x x opposite sin θ = hypotenuse adjacent cos θ = hypotenuse θ = opposite Download our free reference/cheat sheet PDF for trigonometry rules, laws, and identities (with formulas).
In this unit, you'll explore the power and beauty of trigonometric equations and identities, which allow you to express and relate different aspects of triangles, circles, and waves. You'll learn how to use trigonometric functions, their inverses, and various identities to solve and check equations and inequalities, and to model and analyze problems involving periodic motion, sound, light, and. Trig Cheat Sheet Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p <
Trig Identity Cheat Sheet for Maple Learn
Trig Identities Study Sheet This entry was posted on April 3, 2015 by Todd Helmenstine (updated on December 13, 2022) This study sheet has ten groups of trig identities for the basic trigonometry functions. These identities include the reciprocal and co-function relationships between trig functions. The Pythagorean identities are a set of trigonometric identities that are based on the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. The most common Pythagorean identities are: sin²x + cos²x = 1 1 + tan²x = sec²x.



