A present value of 1 table states the present value discount rates that are used for various combinations of interest rates and time periods. A discount rate selected from this table is then multiplied by a cash sum to be received at a future date, to arrive at its present value. Present value (PV) is the current value of a future sum of money or stream of cash flows given a specified rate of return. Future cash flows are discounted at the discount rate, and the higher.

Present Value Tables Double Entry Bookkeeping
The purpose of the present value tables is to make it possible to carry out present value calculations without the use of a financial calculator. They provide the value now of 1 received at the end of period n at a discount rate of i%. The present value formula is: PV = FV / (1 + i) n This can be re written as: PV = FV x 1 / (1 + i)n Answer: Print Table Present Value of $1 ( PVIF) PV = $1 (1 + i)n P V = $ 1 ( 1 + i) n n / i 5.000% 5.125% 5.250% 5 0.78353 0.77888 0.77426 6 0.74622 0.74091 0.73564 7 0.71068 0.70479 0.69895 Present value (PV) is the current value of a stream of cash flows. PV analysis is used to value a range of assets from stocks and bonds to real estate and annuities. PV can be calculated in. Definition: A present value table is a tool that helps analysts calculate the PV of an amount of money by multiplying it by a coefficient found on the table. In other words, it is a table that illustrates the different coefficients that can be used to calculate a figure's present value depending on the discount rate and period of time used.
Present value
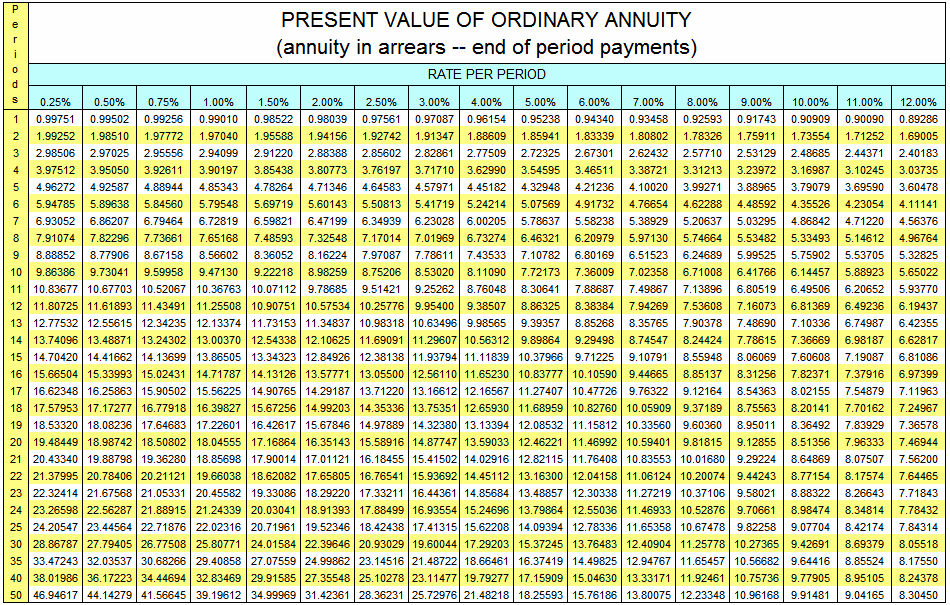
Appendix: Present Value Tables Figure 17.1 Present Value of $1 Figure 17.2 Present Value of Annuity Due (annuity in advance—beginning of period payments) Figure 17.3 Present Value of Ordinary Annuity (annuity in arrears—end of period payments) Previous: 17.6 End-of-Chapter Exercises Net Present Value Analysis with Multiple Investments. A project requiring an investment of $20,000 today and $10,000 one year from today, will result in cash savings of $4,000 per year for 15 years. Find the net present value of this investment using a rate of 10 percent. Round to the nearest dollar. Net Present Value Calculation with Taxes. Present value is what cash flow received in the future is worth today at a rate of interest called the "discount" rate. Here's an easy way to look at present value. If you invest $1,000 in a savings account today at a 2% annual interest rate, it will be worth $1,020 at the end of one year ($1,000 x 1.02). Therefore, $1,000 is the present. A present value table or a PV table lists different periods in the first row and different discount rates in the first column. So, the table provides present value coefficients for a given discount rate and time. In the table, the time can be in weeks, months, or years.
Solved TABLE 4 Present Value of an Ordinary Annuity of 1 1
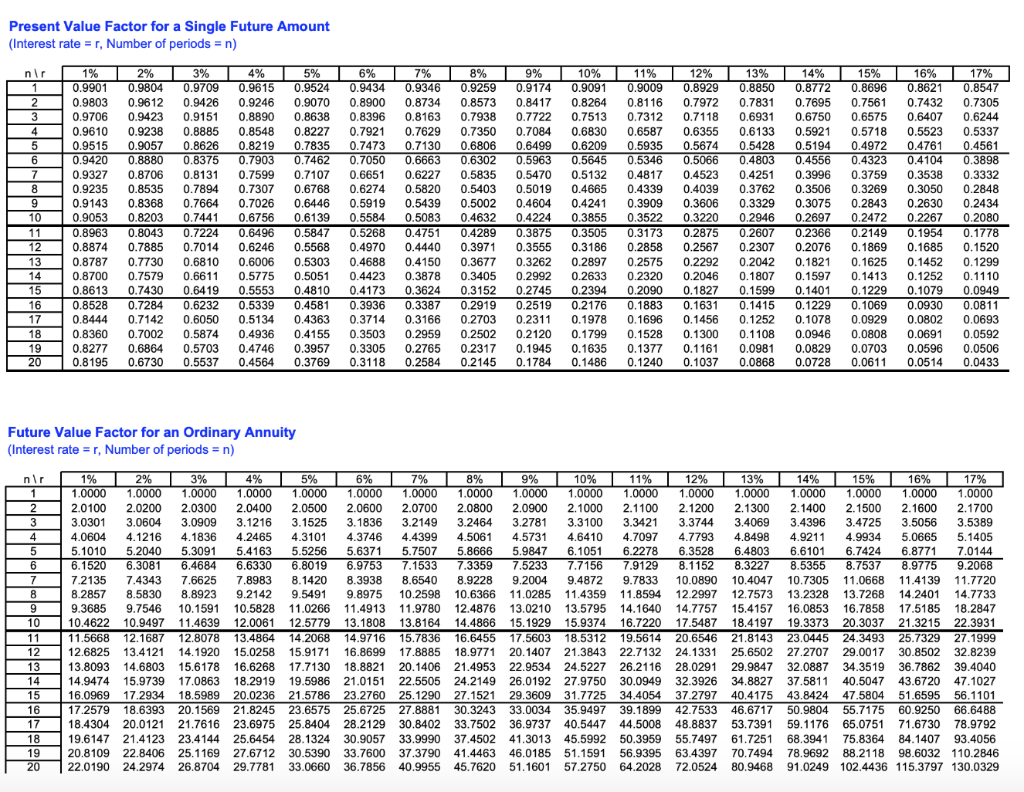
TABLE AI.3 Present Value of $1 Interest Rate 508. TABLE AI.4 Present Value of an Annuity of $1 Interest Rate 509. Title: Appendix I: Future and Present Value Tables Created Date: Present value formula To calculate the present value of future incomes, you should use this equation: PV = FV / (1 + r) where: PV - Present value; FV - Future value; and r - Interest rate. Thanks to this formula, you can estimate the present value of an income that will be received in one year.
Table of Present Value Annuity Factor Number of periods 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 1 0.9901 0.9804 0.9709 0.9615 0.9524 0.9434 0.9346 0.9259 0.9174 0.9091 Present and Future Value Tables (See related pages) Table 1--Future Value of $1 (152.0K) Table 2--Present Value of $1 (152.0K) Table 3--Future Value of an Ordinary Annuity of $1 (157.0K) Table 4--Present Value of an Ordinary Annuity of $1 (153.0K) Table 5--Future Value of an Annuity Due of $1 (157.0K)

Present Value Table Meaning, Important, How To Use It
Calculation Using a PV of 1 Table The present value of receiving $5,000 at the end of three years when the interest rate is compounded quarterly, requires that (n) and (i) be stated in quarters. Use the PV of 1 Table to find the (rounded) present value figure at the intersection of n = 12 (3 years x 4 quarters) and i = 2% (8% per year ÷ 4. Present value is the current value of an asset to be received in the future or the amount that would need to be invested today to receive a specific amount in the future. It accounts for the.



