Diagramming Venn diagram symbols ∪: Union of two sets. A complete Venn diagram represents the union of two sets. ∩: Intersection of two sets. The intersection shows what items are shared between categories. Ac: Complement of a set. The complement is whatever is not represented in a set. What are the symbols of a Venn diagram? For most use cases, we can define a Venn diagram with three symbols: Intersection symbol (∩) Union symbol (U)
Venn Diagram Symbols Steps, Examples & Worksheet
Venn Diagram A Venn diagram is used to visually represent the differences and the similarities between two concepts. Venn diagrams are also called logic or set diagrams and are widely used in set theory, logic, mathematics, businesses, teaching, computer science, and statistics. A Venn diagram is a widely used diagram style that shows the logical relation between sets, popularized by John Venn (1834-1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses simple closed. What are Venn diagram symbols? Venn diagram symbols are a collection of mathematical symbols that are used within set theory. Venn diagrams were created by mathematician John Venn and are used widely today within computer sciences, problem-solving and set theory. To create a Venn diagram, first we draw a rectangle and label the universal set " U = Plants. U = Plants. " Then we draw a circle within the universal set and label it with the word "Trees." Figure 1.7 This section will introduce how to interpret and construct Venn diagrams.

Venn Diagram Symbols and Notation Lucidchart
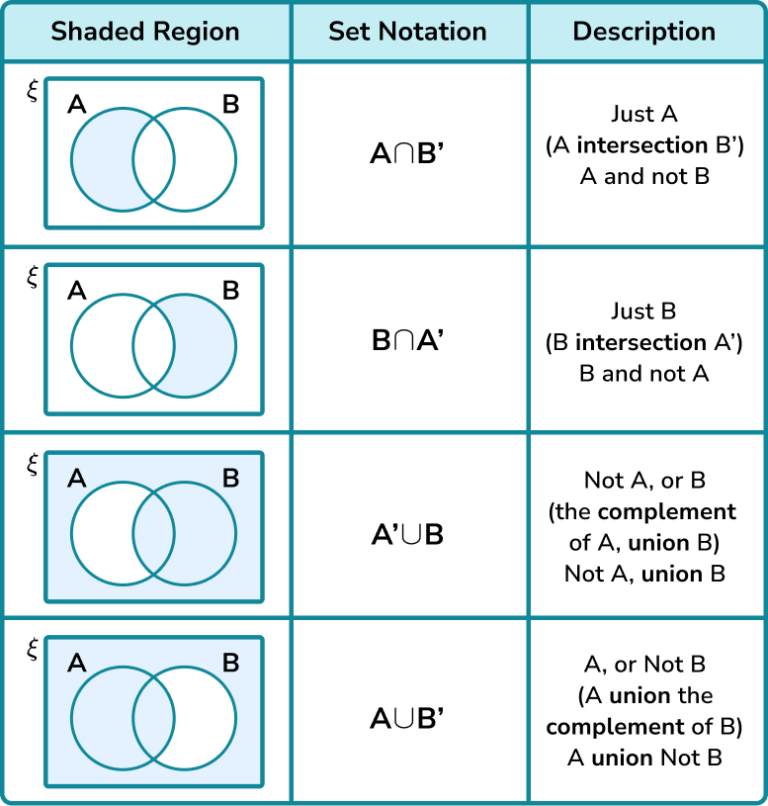
Each individual set within a Venn diagram is usually represented by a circle or an oval and is labeled with an uppercase letter. These labels help differentiate between the sets when describing the relationships and operations performed on them. Intersection Symbol (∩) The intersection symbol '∩' is vital in understanding shared characteristics. Venn diagrams consist of a series of overlapping circles, each circle representing a category. To represent the union of two sets, we use the ∪ symbol — not to be confused with the letter 'u.' In the below example, we have circle A in green and circle B in purple. This diagram represents the union of A and B which we notate as A ∪ B. A Venn diagram begins with a box called our universal set, which is denoted by the symbol \(ε\) (epsilon). The universal set contains everything we are interested in at that particular time. Venn diagrams are a visual way of representing sets . They consist of one or more circles inside a rectangle. The circles usually overlap. All the data being considered is contained inside the.

Símbolos de Diagrama Venn y Notación Gráfico Lúcido Mex Alex
T means the set of Tennis players. V means the set of Volleyball players. The Venn Diagram is now like this: Union of 3 Sets: S ∪ T ∪ V. You can see (for example) that: drew plays Soccer, Tennis and Volleyball. jade plays Tennis and Volleyball. alex and hunter play Soccer, but don't play Tennis or Volleyball. no-one plays only Tennis. This is a Venn diagram Below using two sets, A and B. This is a Venn diagram using sets A, B and C. Study the Venn diagrams on this and the following pages. It takes a whole lot of practice to shade or identify regions of Venn diagrams.
A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set. In the above figure, we can see a Venn diagram, represented by a rectangular shape about the universal set, which has two independent sets, X and Y. Here are the four simple steps for drawing a Venn diagram: Step 1: Sort all of the elements into sets. Step 2: Make a rectangle and name it according to the relationship between the sets. This represents the universal set. Step 3: Draw as many circles as the variety of groups or sets.

Venn Diagrams Video Corbettmaths
Venn diagrams can be used to express the logical (in the mathematical sense) relationships between various sets. The following examples should help you understand the notation, terminology, and concepts relating Venn diagrams and set notation. Let's say that our universe contains the numbers 1, 2, 3, and 4, so U = {1, 2, 3, 4}. Venn Diagrams are used to represent the groups of data in circles, if the circles are overlapping, some elements in the groups are common, if they are not overlapping, there is nothing common between the groups or sets of data.




