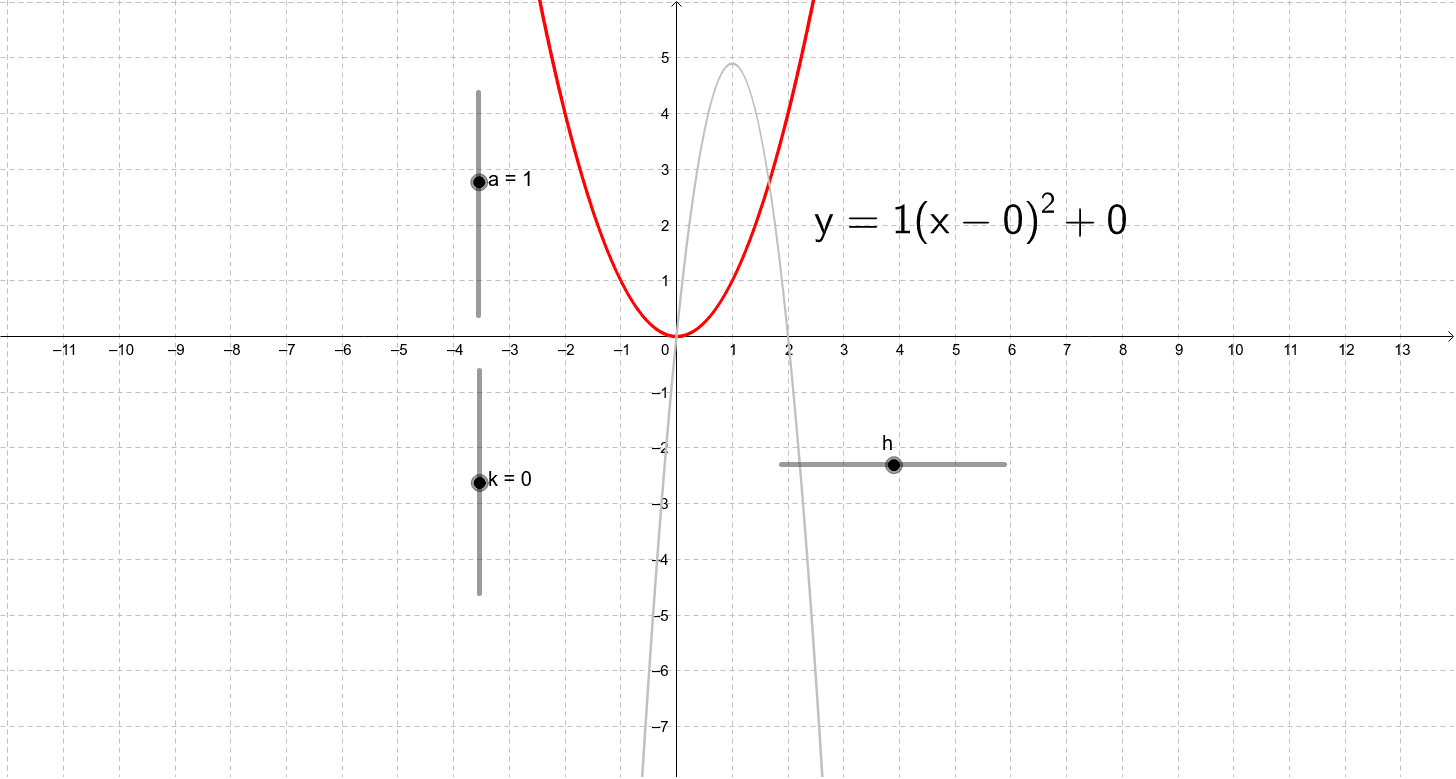Let us convert it to the vertex form y = a(x - h) 2 + k by completing the squares. Subtracting c from both sides: y - c = ax 2 + bx. Taking "a" as the common factor: y - c = a (x 2 + b/a x) Here, half the coefficient of x is b/2a and its square is b 2 /4a 2. Adding and subtracting this on the right side (inside the parentheses): Typically, we denote the vertex as a point P (h,k), where h stands for the x-coordinate, and k indicates the y-coordinate. That's enough on the definitions. But how to find the vertex of a quadratic function? It may be a surprise, but we don't need to evaluate any square root to do so!
y=a(xh)^2+k GeoGebra
To convert a quadratic from y = ax2 + bx + c form to vertex form, y = a ( x - h) 2 + k, you use the process of completing the square. Let's see an example. Convert y = 2x2 - 4x + 5 into vertex form, and state the vertex. Here's a sneaky, quick tidbit: When working with the vertex form of a quadratic function, and . Parabola Opens Right. Standard equation of a parabola that opens right and symmetric about x-axis with vertex at origin. y 2 = 4ax. Standard equation of a parabola that opens up and symmetric about x-axis with at vertex (h, k). (y - k) 2 = 4a(x - h) Graph of y 2 = 4ax : The parabola is the curve formed from all the points (x, y) that are equidistant from the directrix and the focus. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola up the middle) is called the axis of symmetry. Graph the parabola given by the equation y = ( x − 2) 2 + 3. Step 1: Comparing the equation to the general vertex form y = a ( x − h) 2 + k of a parabola, we see that h = 2 and k = 3.

Standard Form of Circle Equation Expii
Identify the vertex and axis of symmetry for a given quadratic function in vertex form. The standard form of a quadratic function presents the function in the form. f (x)= a(x−h)2 +k f ( x) = a ( x − h) 2 + k. where (h, k) ( h, k) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also. Pre-Algebra. Solve for y (y+k)h=C. (y + k)h = C ( y + k) h = C. Divide each term in (y+k)h = C ( y + k) h = C by h h and simplify. Tap for more steps. y+k = C h y + k = C h. Subtract k k from both sides of the equation. y = C h −k y = C h - k. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. The vertex form of a parabola's equation is generally expressed as: y = a ( x − h) 2 + k. (h,k) is the vertex as you can see in the picture below. If a is positive then the parabola opens upwards like a regular "U". If a is negative, then the graph opens downwards like an upside down "U". And, just like standard form, the larger the | a. vertical: y=a(x-h) 2 +k horizonal: x=a(y-k) 2 +h Often parabolas are already listed in this format, but sometimes they are not. In this case, you must put them into the graphing format by completing the square. To complete the square for a parabola, follow these steps: 1. Identify which variable is squared.

AMLnZuhKJUtseaei0fLqmgTkU5nmoFYDFPj5Ly0r2=s900ckc0x00ffffffnorj
Step-by-Step Guide on How to Graph a Parabola. 1. Identify the concavity of the parabolic equation. Refer to the table above for the directions of the opening of the curve. It could be opening to the left or right, or upward or downward. 2. Locate the vertex of the parabola. The vertex can either be (0, 0) or (h, k). Explanation: General equation of parabola is of the form y = a(x − h)2 +k or x = a(y − k)2 +h. Former is known as verticle parabola and latter is known as horizontal parabola. In both cases vertex is (h,k), axis of symmetery is x −h = 0 in former case and y −k = 0 in latter case.
Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step Which is a fancy way or a mathematical model that an economist might use to tie the factors of production in an economy to the actual aggregate output of an economy. The aggregate output is Y. And then the factors of production, we've talked about this before, it's human capital, it's technology, and it is regular capital, or non-human capital.

Y.K.H youtube YouTube
$\begingroup$ What you are proposing in comparing to finite difference methods vs. linear multi-step or Galerkin methods is what Heun did in 1900 just prior to Kutta in 1901. He took chains of Euler-like steps and only combined their final values in a linear combination. This gives much more flexibility to satisfy the order conditions, at the cost of more function evaluations. Click Here REVORING Swift System Lightning-fast Installation Click Here Goodbye Step-up Rings H&Y REVORING Click Here The future of Filters K-series Magnetic Filter Holder System H&Y Filters Upwork 2022-12-30T15:16:35+08:00