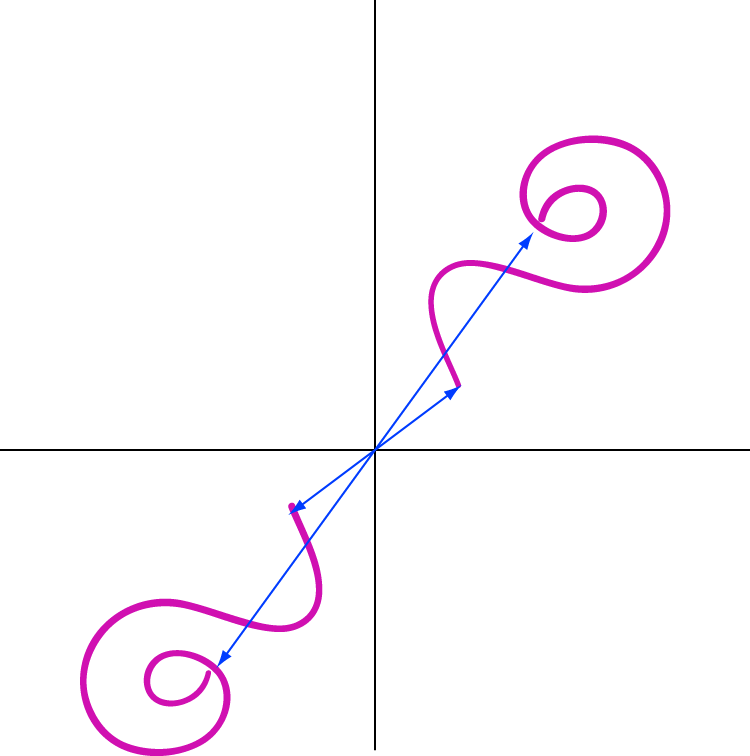
Point Symmetry. Point Symmetry is when every part has a matching part: the same distance from the central point. but in the opposite direction. It is also the same as "Rotational Symmetry of Order 2". Note: Point Symmetry is sometimes called Origin Symmetry, because the "Origin" is the central point about which the shape is symmetrical. Point Symmetry, or Origin Symmetry, or Central Symmetry is a type of symmetry where an object or shape looks the same when rotated 180° (a half-turn) around a central point. In this article, we will discuss Point Symmetry in detail including its definition, examples, as well as some real-life examples in nature as well.
Point Symmetry Prekinder to Grade 2 Mathematics
A point of symmetry is a point that represents a "center" of sorts for the figure. For any line that you draw through the point of symmetry, if this line crosses the figure on one side of the point, the line will also cross the figure on the other side of the point, and at exactly the same distance from the point. Symmetry. In geometry, symmetry describes the balance a figure has. A figure or object has symmetry if a transformation (s) maps it back onto itself. Both plane and space figures may have symmetry. There are three basic types of symmetry: reflection, rotation, and point symmetry. Point Symmetry. more. Where every part has a matching part the same distance from the central point but in the opposite direction. It looks the same when viewed from opposite directions (after a 180° rotation). Also called Origin Symmetry, and is identical to "Rotational Symmetry of Order 2". Illustrated definition of Point Symmetry: Where. Rotational symmetry: When an object is rotated in a particular direction, around a point, then it is known as rotational symmetry. Reflexive symmetry: Reflective symmetry, also called mirror symmetry, is a type of symmetry where one half of the object reflects the other half of the object.

Symmetry Definition Solved Examples Geometry Cuemath
So, the point with which the rectangle is rotated is called the point of symmetry. Solved Example on Point of Symmetry Ques: Which of the figures has a point of symmetry? Choices: A. Graph 1 B. Graph 2 C. Graph 3 D. none of the above Correct Answer: A. Solution: Step 1: A figure or a graph when rotated by 180° looks similar to its original, it. A special center point for certain kinds of symmetric figures or graphs . If a figure or graph can be rotated 180° about a point P and end up looking identical to the original, then P is a point of symmetry. Example: This is a graph of the curve together with its point of symmetry (-2, 1). The point of symmetry is marked in red. What is Point Symmetry? Point symmetry is when, given a central point on a shape or object, every point on the opposite sides is the same distance from the central point. Other terms for point. Point symmetry in a shape occurs when there is a central point on an object such that: The central point divides the shape into two parts or sides, Part 1 and Part 2. Every point on Part 1 must have a matching point on Part 2 equidistant from the central point. Point Symmetry is also called Origin Symmetry , since the 'Origin' is the.
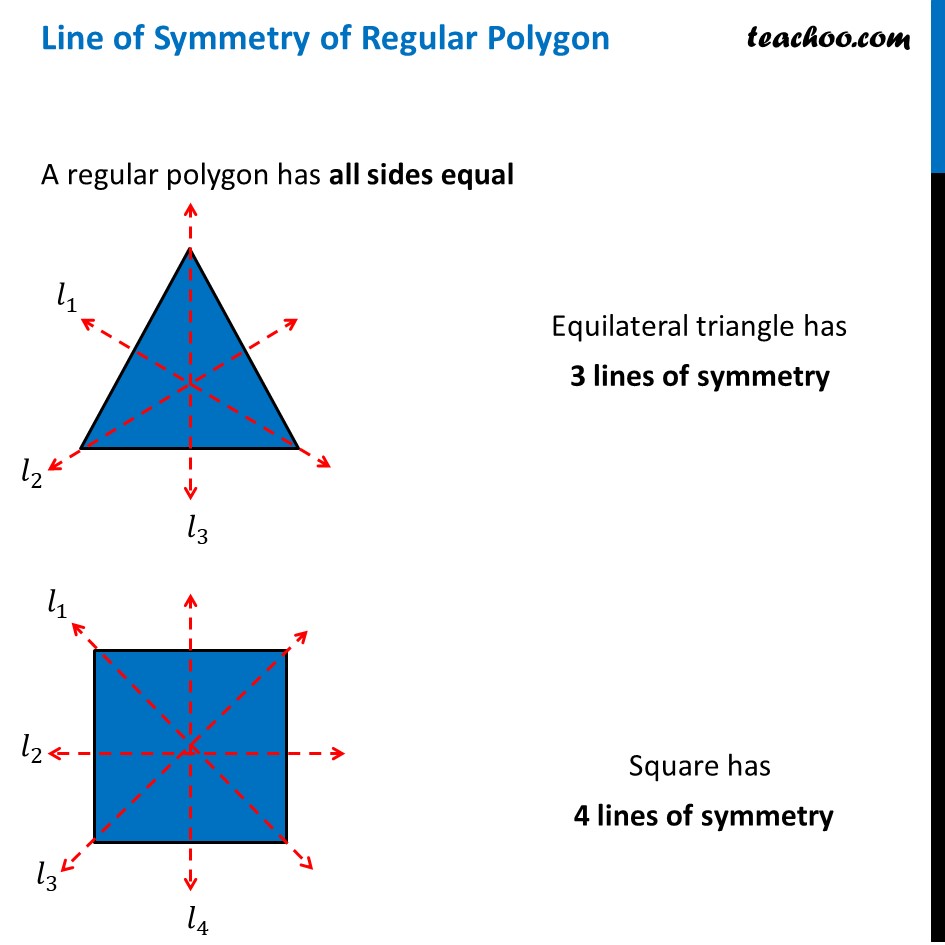
Line of Symmetry of Regular Polygon [with Formula and Examples]
So, a function can never be symmetrical around the x-axis. Just remember: symmetry around x-axis ≠ function. To answer your second question, "even" and "odd" functions are named for the exponent in this power function: f (x) = xⁿ. - if n is an even integer, then f (x) is an "even" function. - if n is an odd integer, then f (x) is an "odd. So our vertex right here is x is equal to 2. Actually, let's say each of these units are 2. So this is 2, 4, 6, 8, 10, 12, 14, 16. So my vertex is here. That is the absolute maximum point for this parabola. And its axis of symmetry is going to be along the line x is equal to 2, along the vertical line x is equal to 2.
Point Symmetry: In geometry, there are different aspects associated with symmetry, and students need to understand the concept of symmetry. This concept is used by artists, professionals, clothes and jewellery designers, automobile manufacturers, architects, and others for different tasks associated with their respective professions. What is Point Symmetry? A figure has point symmetry if it has a rotational symmetry of 180 degrees. One way to check if a figure has point symmetry would be to turn it upside down. If the figure looks the same as the original then it has point symmetry. The following figures have point symmetry:

Lines and Points of Symmetry If there is a common point ofpehs. Symmetry Lines and Points of
From other geometry videos and lessons we have learned about similarity and congruency in polygons, particularly triangles. In these lessons we intuitively learned that the position of the polygons did not matter when it comes to proving similarity and congruency. I.e. if two triangles are rotated 90 degrees from each other but have 2 sides and. Two points z and z^S in C^* are symmetric with respect to a circle or straight line L if all circles and straight lines passing through z and z^S are orthogonal to L. Möbius transformations preserve symmetry. Let a straight line be given by a point z_0 and a unit vector e^(itheta), then z^S=e^(2itheta)z-z_0^_+z_0, where z^_ is the complex conjugate.




