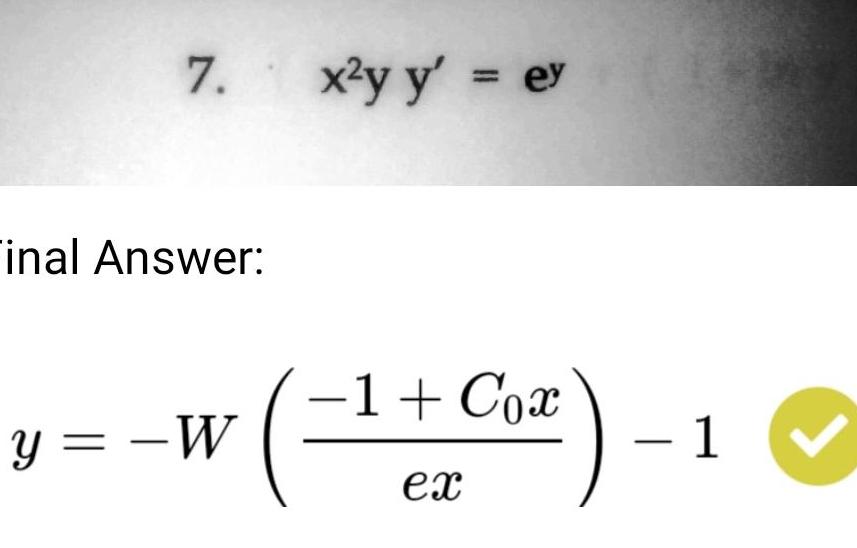Basic Math Solve for y w=x+xyz w = x + xyz w = x + x y z Rewrite the equation as x+xyz = w x + x y z = w. x+xyz = w x + x y z = w Subtract x x from both sides of the equation. xyz = w−x x y z = w - x Divide each term in xyz = w −x x y z = w - x by xz x z and simplify. Tap for more steps. y = w xz − 1 z y = w x z - 1 z Linear Equation y = −wx Similar Problems from Web Search y = −x + 1 http://www.tiger-algebra.com/drill/y=-x_1/ y=-x+1 Geometric figure: Straight Line Slope = -2.000/2.000 = -1.000 x-intercept = 1/1 = 1.00000 y-intercept = 1/1 = 1.00000 Rearrange: Rearrange the equation by subtracting what is. y = −x + 4 http://www.tiger-algebra.com/drill/y=-x_4/

Poniżej przedstawiono fragment wykresu funkcji y = W(x), gdzie W(x
Lambert W function The product logarithm Lambert W function plotted in the complex plane from −2 − 2i to 2 + 2i The graph of y = W(x) for real x < 6 and y > −4. The upper branch (blue) with y ≥ −1 is the graph of the function W0 (principal branch), the lower branch (magenta) with y ≤ −1 is the graph of the function W−1. Arithmetic Matrix Simultaneous equation Differentiation Integration Limits Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more. Solve for y w=(x-y)/2-z. Step 1. Rewrite the equation as . Step 2. Simplify . Tap for more steps. Step 2.1. To write as a fraction with a common denominator, multiply by . Step 2.2. Combine and . Step 2.3. Combine the numerators over the common denominator. Step 2.4. Multiply by . Step 3. Multiply both sides by . Step 4. Differentiation. dxd (x − 5)(3x2 − 2) Integration. ∫ 01 xe−x2dx. Limits. x→−3lim x2 + 2x − 3x2 − 9. Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more.

Powtórka przed maturą matematyka zadania 42_8 Na rysunku obok
Send us Feedback. Free derivative with respect to (WRT) calculator - derivate functions with respect to specific variables step-by-step. Linear equation. Arithmetic. Matrix. Simultaneous equation. Differentiation. Integration. Limits. Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more. The angle opposite of the hypotenuse is ninety degrees. The angle opposite of the short leg is forty degrees. The angle opposite of the long leg is fifty degrees. W Y W X . A right triangle W X Y. Angle Y is a right angle. Angle W is seventy degrees. Choose 1 answer: (Choice A) 0.34 . Because when you write "w" (and implicitly are thinking of x, y and z as functions of u and v) you are already thinking of w \cdot f. No difference between the two. Handling undefined case in uniqueness proof (How to Prove It, Velleman; 5.6, 2)
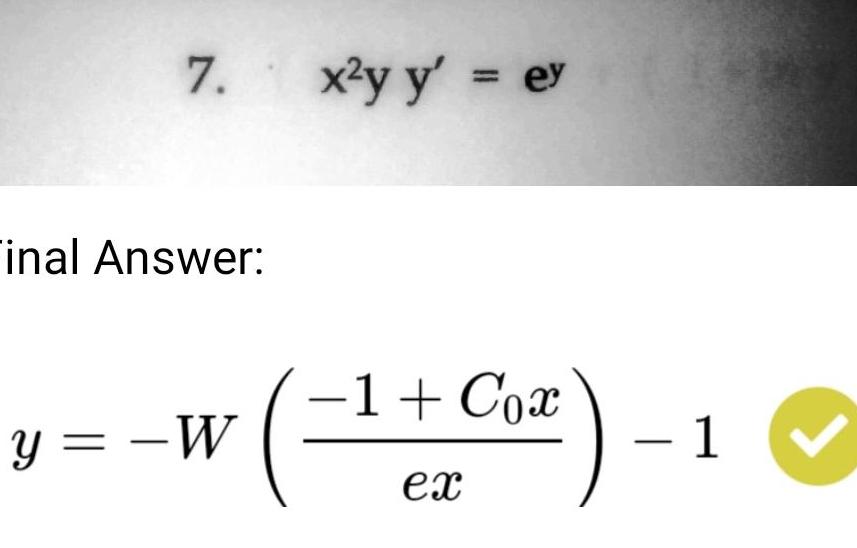
[ANSWERED] 7 inal Answer y W x y y ey 1 Cox ex 1... Calculus
初のホールツアー『Tani Yuuki Hall Tour 2023 "kotodama"』開催! ツアー名Tani Yuuki Hall Tour 2023 "kotodama" 開催日時・場所11月3日(祝金) 東京・東京国際. This video is Part 5 of the Alphabet ABC Phonics Series, covering letters V, W, X, Y, and Z. This series goes through each of the letters, starting with A an.
「THE FIRST TAKE」は、一発撮りのパフォーマンスを鮮明に切り取るYouTubeチャンネル。 ONE TAKE ONLY, ONE LIFE ONLY. 一発撮りで、音楽と向き合う。第203回は. The steps are justified by distributivity (which apparently you are already used to) and the laws: a +a′ = 1 and a1 = a, a + a ′ = 1 and a 1 = a, for each a a, and the usual idempotence, commutativity and associativity. I suppose you can fill in these justifications. Share. Cite.

Fichas de lectoescritura con las letras W y X
Get Step by Step Now. Starting at $5.00/month. Get step-by-step answers and hints for your math homework problems. Learn the basics, check your work, gain insight on different ways to solve problems. For chemistry, calculus, algebra, trigonometry, equation solving, basic math and more. 1 Starting from (W + Y) (W' + X' + Y) (X' + Y' + Z') (you have already solved till this point) let Y=A, B=W and C= (W'+X') for next step using (A+B) (A+C)= (A+BC); = (Y+W (W'+X')) (X' + Y' + Z') = (Y+WW'+WX') (X' + Y' + Z') // WW'=0 = (Y+WX') (X' + Y' + Z') //simplified by removing WW'=0 = (Y+W) (Y+X') (X' + Y' + Z') // used (A+B) (A+C)=A+BC