Desarrollo de cono La calculadora calcula el barrido (patrón) en el plano de un cono circular recto y un cono circular recto truncado La calculadora calcula los parámetros de barrido de un cono circular derecho en un plano. La siguiente imagen ilustra la tarea. DESARROLLO DE CUERPOS GEOMÉTRICOS. CONOS o CONO TRUNCADO 18 o CONO TRUNCADO 19 . 2 TETRAEDRO . 3 HEXAEDRO O CUBO . 4 OCTAEDRO . 5 DODECAEDRO . 6 ICOSAEDRO . 7 PRISMA TRIANGULAR . 8 PRISMA CUADRANGULAR: Este ejemplo se denomina PARALELEPÍPEDO porque las bases son paralelogramos. 9

Tutorial de dibujo │ Desarrollo de un cono YouTube
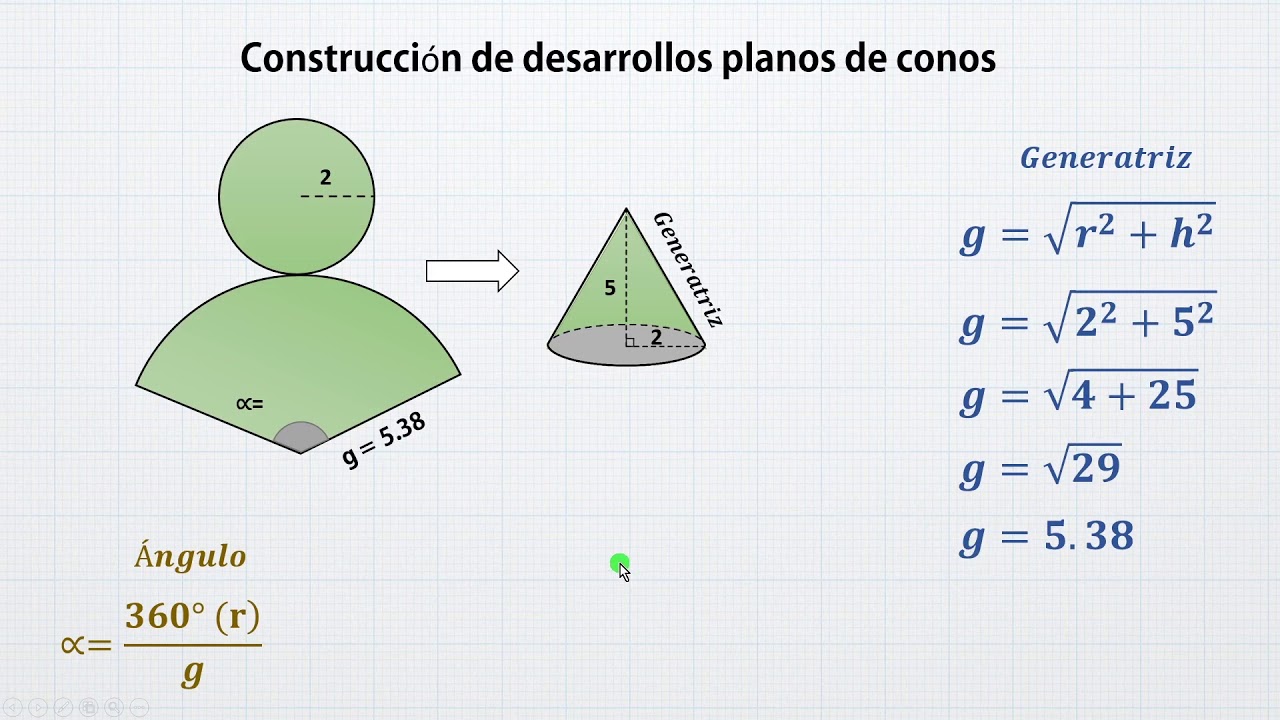
Desarrollo plano del cono. El desarrollo plano de un cono recto es un sector circular y un círculo. El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base. En este video veremos la teoría y desarrollo para realizar cualquier cono a medida deseada, usando solo una fórmula simple.Como trazar angulos.https://youtu.. El cono completamente desarrollado en un plano, lo que llamamos desarrollo plano del cono: Para calcular el área o superficie lateral de un cono necesitamos conocer la generatriz, es decir, la distancia entre el vértice y uno de los puntos de la circunferencia de la base. Pilar LC 318 subscribers Subscribe 233 Share 16K views 3 years ago Matemáticas 3 Secundaria En éste video explico como diseñar un desarrollo plano de un cono para el tema Análisis de las.
Desarrollo de un cono. Área del cono. GeoGebra
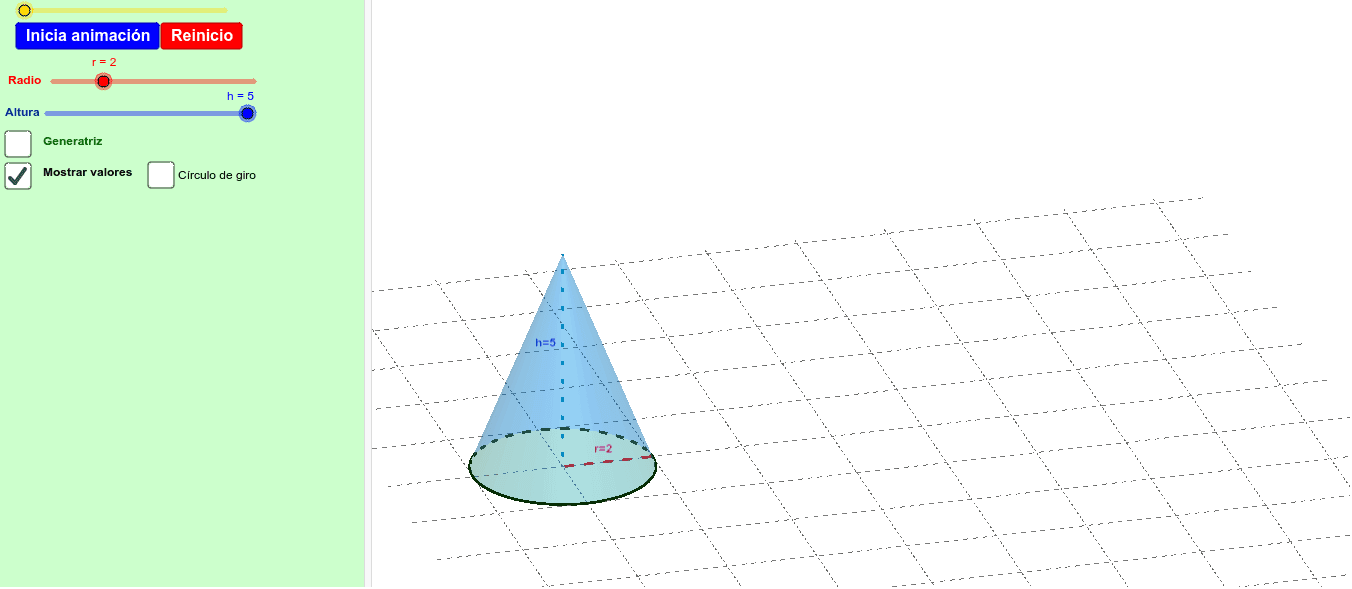
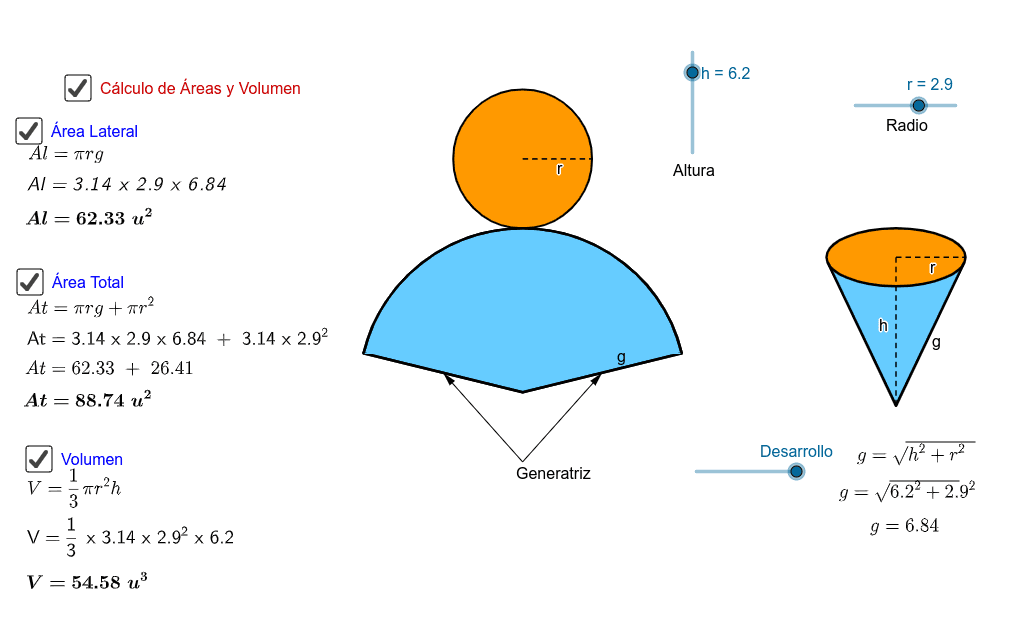
Desarrollo del cono El desarrollo plano de un cono recto es un sector circulary un círculo. El sector circularestá delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base. En la siguiente imagen observa lo que sucede al variar el radio y la altura del cono: « Anterior| Siguiente» Desarrollo de un cono. Área del cono. Autor: Leopoldo Aranda Murcia. Tema: Área, Cono. Pulsado el botón "Inicia animación" se desarrolla el cono y además se va explicando cómo se calcula su área lateral y el área de su base. Nuevos recursos. Mapa mudo; 1º CIENCIAS 2º C. SOCIALES 2º CIENCIAS Cono. Llamamos cono al cuerpo de revolución engendrado por un triángulo rectángulo al girar alrededor de uno de sus catetos. Elementos del cono : Eje : cateto sobre el que gira el triángulo para generar el cono. Altura : longitud del eje. Generatriz : Longitud de la hipotenusa del triángulo. Desarrollo del cono y cálculo de Área lateral, Área total y Volumen. Nuevos recursos. Mapa mudo; Mosaico 1; A ojo de buen cubero; Teorema de los Cículos de Descartes; Un paseo por Sierpinski; Descubrir recursos. Distancia entre dos puntos; test; animaciones de graficas;
Desarrollo del plano de cono y transformación de triangulo a cono YouTube
DESARROLLO PLANO DE UN CONO | EJERCICIO Mate 123 4.45K subscribers Subscribe Subscribed 6 Share 124 views 1 year ago PAPANTLA DE OLARTE #Aprendeencasa #Matematicas #Edutubers. 14:48 ET (19:48 GMT) 5 enero, 2024. ¿En qué beneficia a Argentina su entrada al grupo BRICS? 0:54. (CNN Español) - El bloque BRICS es una alianza económica, política y social integrada por.
Desarrollo del cono de revolución oblicuo. Desarrollamos un cono auxiliar de sección recta, la generada en el cono dado por el plano Q perpendicular al eje, tomado arbitrariamente. Dividimos en un número cualquiera de partes iguales (ocho en el ejemplo) la base reabatida del cono auxiliar tomado y el sector circular resultante de su desarrollo. Desarrollo de cono. Radio de la base r₂. Altura del cono H. Segundo radio de la base r₁. Segundo radio de la base (en caso de tronco - cono truncado) Cálculo preciso. Dígitos después del punto decimal: 2. Altura inclinada L. Radio de arco inferior R₂.
Desarrollo, Área y Volumen del cono GeoGebra
Calculos para el trazado del desarrollo de un cono pdf. Calculos para el trazado del desarrollo de un cono. Se peresenta el calculo para el trazado de un desarrollo de un cono; con las formulas; para llevarlo acad; y poder cortar un cono; si es truncado se tiene que calcular el radio menos. Desarrollo del cono. Autor: Josep Font Jiménez. Tema: Cono. Nuevos recursos. Un paseo por Sierpinski; El repartidor de pizza; Cuadriláteros cíclicos ortodiagonales; Teorema de los Cículos de Descartes; El triángulo órtico y la circunferencia circunscrita; Descubrir recursos. Seno de la suma de ángulos. Demostración




