El eje radical de las circunferencias O3 y O2 se calcula como el de dos circunferencias tangentes exteriores, donde una de ellas tiene radio 0, el eje radical pasará por el punto de tangencia y será perpendicular a la línea de centros. Por el punto de intersección de los dos ejes radicales se traza una perpendicular a la línea de centros. Suscríbete: http://bit.ly/1u5LQ0MWeb de matemáticas gratis: http://bit.ly/1owtgabExplicaremos como encontrar el eje radical de dos circunferencias, que es la.

Eje Radical de dos Circunferencias Exteriores Método fácil YouTube
Construcción del eje radical. (El eje radical de dos circunferencias no concéntricas) Dibujemos una circunferencia que corte a las circunferencias C 1 y C 2, en A, A ′ y B, B ′. Sea P la intersección de A A ′ y B B ′, dibujamos la perpendicular a la línea de los centros de las circunferencias dadas. La perpendicular es el eje. Eje radical. En geometría plana, el eje radical de dos circunferencias no concéntricas es el lugar geométrico de los puntos con igual potencia respecto de las mismas. Por medio de la geometría analítica se puede demostrar que el eje radical es siempre una recta. Sean y los centros de los dos círculos, y los radios correspondientes. En este vídeo tutorial vamos a aprender a dibujar el eje radical de dos circunferencias en diferentes casos: Circunferencias exteriores (0:13), circunferenci. El eje radical de dos circunferencias es el lugar geométrico de todos los puntos que constituyen dicho eje tienen la misma potencia con relación a ambas. Las circunferencias pueden ser exteriores como representamos a continuación: Las circunferencias son C1 y C2. Las unimos por el centro con una recta. La circunferencia C3 trazamos teniendo.

Polar, centro y eje radical 10endibujo
Curso de Dibujo Técnico: https://educale.com El eje radical de dos circunferencias es el lugar geométrico de los puntos del plano que tienen igual potencia r. 1) Halla el eje radical de las siguientes circunferencias. a ) C 1 : x² + y ² + 2x - 3y + 1 = 0 b ) C 2 : x² + y ² + 5x = 0 Comprueba que es una recta perpendicular a la línea de sus centros. 2) Halla el eje radical de las siguientes circunferencias. a ) C 1 : x² + y² - 8 = 0 b ) C 2 : 2x² + 2y² - 3x - 8y - 5 = 0 Eje radical de dos circunferencias. Para poder determinar el eje radical de dos circunferencias primero tenemos que analizar las distintas posiciones que pueden ocupar en el plano: secantes, tangentes y exteriores. En la siguiente animación puedes cómo queda dispuesto el eje radical de dos circunferencias según estén dispuestas. Obtención algebraica del eje radical de dos circunferencias (no concéntricas): El eje radical es el lugar geométrico de los puntos del plano que tienen la misma potencia respecto de dos circunferencias fijas.Expresión analítica de la potencia de un punto respecto de una circunferencia de centro y radio : Si la ecuación de la circunferencia es la siguiente: , la potencia del punto P se.
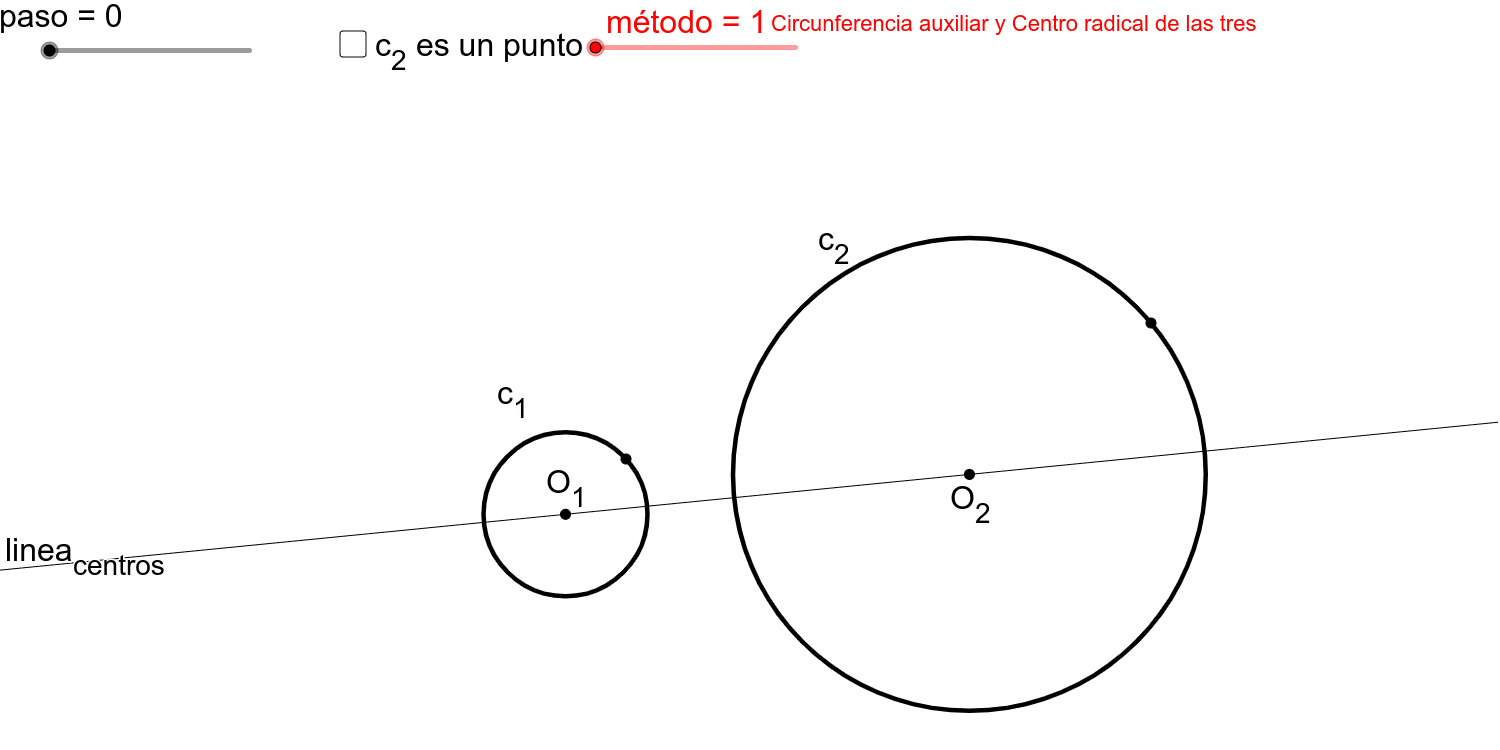
Determinación del eje radical de dos circunferencias GeoGebra
En este vídeo tutorial vamos a aprender a dibujar de manera sencilla el eje radical a dos circunferencias exteriores, sabiendo que debe ser perpendicular a l. Explicación y cálculo del eje radical de dos circunferencias conociendo la ecuación de las dos circunferencias mediante un ejemplo#Auxi #matemáticas #Matemat.
WEB: http://profesordedibujo.com/TWITTER: http://twitter.com/ProfedeDibujoFACEBOOK:http://www.facebook.com/PDDProfesorDeDibujoSi te resultó útil: dale a "me. Curso de Dibujo Técnico: https://educale.com El procedimiento es igual al de dos circunferencias exteriores.Se unen los centros entre sí.Entre las circunfere.

Eje radical de DOS CIRCUNFERENCIAS INTERIORES YouTube
Recuerda que: L a recta que une los centros de dos circunferencias será siempre perpendicular al eje radical. Centro radical. El centro radical es el punto que tiene la misma potencia respecto a tres circunferencias. Se obtiene hallando la intersección de los ejes radicales de cada circunferencia. El eje radical de dos circunferencias no concéntricas esta formado por los puntos cuya potencia es la misma respecto a las dos circunferencias. (Lugar geométrico de los puntos del plano que tienen igual potencia respecto a las dos circunferencias). Se demuestra que este lugar geométrico es una recta perpendicular a la que une los centros de.




