Calculadora del volumen de un tronco de pirámide. Introduce los datos del tronco de pirámide y luego pulsa el botón «Calcular» para hallar el volumen del cuerpo geométrico. Debes introducir los números en centímetros utilizando el punto como separador decimal. Área de la base mayor =. Área de la base menor =. Altura =. Tienes que sacar el volumen total. Tienes la fórmula y los datos para hallarlo. Saca los 4/7 y tendrás el volumen de digamos un tronco de base 30 x 30 y menos altura. Con el área de la base menor y los cuatro trapecios que estarán en contacto con el agua, sacarás la superficie humedecida que te piden.

formula del volumen del tronco de piramide urgente Brainly.lat
Volumen del tronco de la pirámide es: Antigua fórmula para calcular el volumen de un tronco de pirámide: Si deseas calcular directamente el valor del volumen de un tronco de pirámide aplicas la fórmula: Aplicando a este ejercicio tendremos: 15 (3).31 Calcula: 1) apotema de la base inferior 2) apotema de la base superior 3) área de la base. www.matematicasyeso.es ----- Sigue los vídeos en orden desde esta webEn este vídeo vamos a aprender a calcular el volumen de un tronco de pirámide. El tronco de pirámide es un poliedro formado por dos caras paralelas, que son las bases, y varias caras laterales, que son trapecios.Ambas bases tienen el mismo número de lados y tiene tantas caras laterales como lados tienen sus bases. Está formado por el sólido inferior resultante de seccionar una pirámide con un plano intermedio y paralelo a su base. Aprende a calcular el VOLUMEN de un TRONCO de PIRÁMIDE.SERIE sobre CUERPOS GEOMÉTRICOS 👉 https://youtube.com/playlist?list=PLiWRH3aE37VLV90nDzDbOCFHWr8HyRvp.
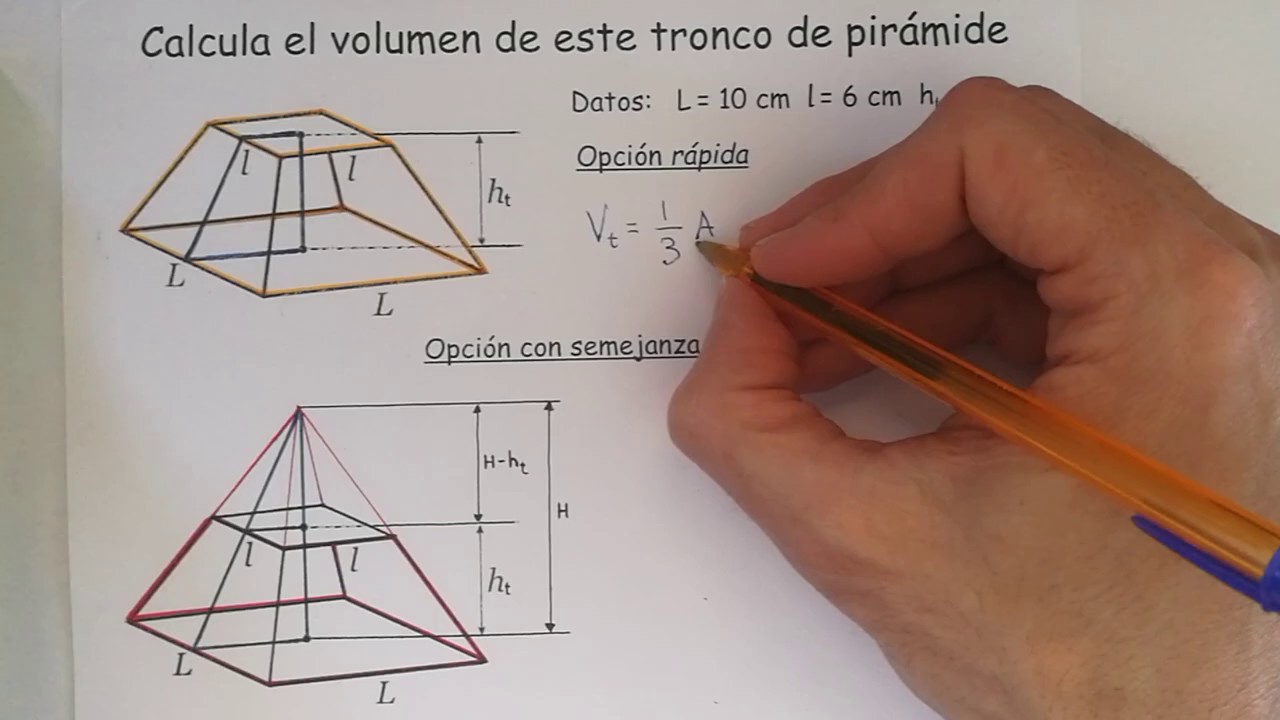
Volumen de un tronco de pirámide (forma rápida o aplicando semejanza) YouTube
¿Necesitas revisar algún otro tema? ¿algún otro nivel? No te pierdas este enlace con T O D O 🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻🔻 🔵 https://vi. Para calcular el volumen del tronco piramidal se utilizará la siguiente expresión ( h es la altura, A es el área de la base y A ′ el área de la base menor) V = h 3 ( A + A ′ + A ⋅ A ′) Dicho volumen tiene un valor de V = 55, 5 m 3. Es el poliedro resultante de realizar un corte paralelo a la base de una pirámide. Fórmulas: área y volumen. Ahora veremos cómo calcular el volumen y el área de un tronco de pirámide. Primero denotemos algunos elementos básicos del tronco. Dado esto, ahora presentamos las fórmulas para el área lateral, área total y el volumen de un tronco de pirámide. Respuesta: Solución. Hallamos el volumen de un prisma que tenga por base un cuadrado de 2 cm. de lado y 4,5 cm. de altura y como en un prisma caben 3 pirámides iguales, al resultado lo dividimos por 3: 15 (3).27 La pirámide Keops de Egipto tiene una base cuadrada de 230 metros de lado. Sabemos que el volumen de dicha pirámide es de .

2º ESO Área y volumen de un tronco de pirámide YouTube
Solución. Dibuje una figura. La fórmula para el volumen de una pirámide es, Ya que la base de la pirámide es un cuadrado, el área de la base es 10 2 o 100 cm 2 . Así, sustituya 100 por B y 18 por h en la fórmula. Por lo tanto, el volumen de la pirámide cuadrada es de 600 cm 3 . El volumen de una pirámide es un tercio del área de la base de la pirámide (A b) y su altura (h). ¿Cómo se obtiene esta fórmula? El volumen de una pirámide recta y de una pirámide oblicua de igual altura es el mismo si al ser cortadas por cualquier plano paralelo a sus bases se producen en ellas secciones de igual área, aplicando el principio de Cavalieri .
Duración: 15:00. Calcular el área y el volumen de un tronco de pirámide de bases cuadradas de lados 6 y 4 cm y de apotema 8 cm. Formula tronco piramide. Formula tronco cono. Volumen tronco cono mediante triangulos semejantes. Triangulos semejantes. INICIO; E.S.O. Bachillerato; Álgebra; Cálculo; Funciones;. Calcula el volumen de un tronco de cono de 10 cm de altura, conociendo que los radios da las bases miden 3 y 8 cm.
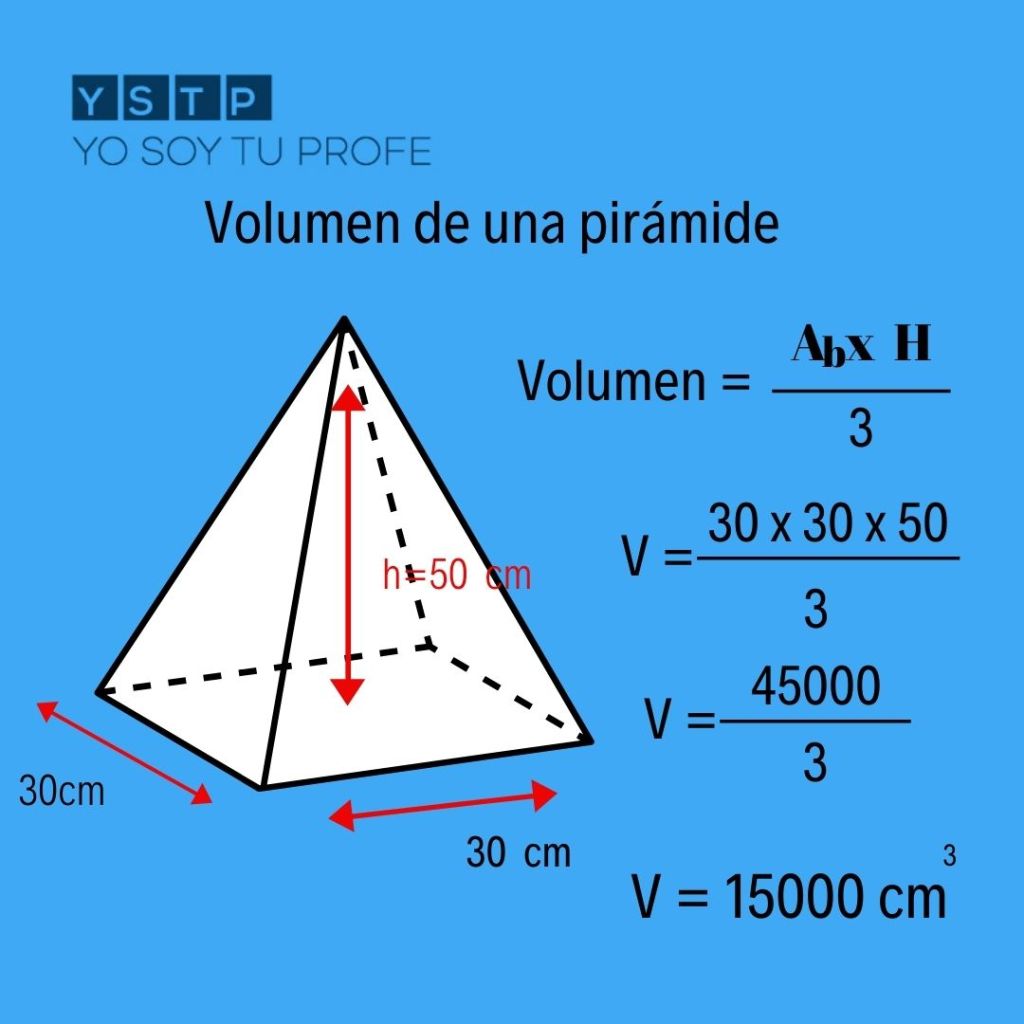
¿Sabes calcular el volumen de una pirámide? Yo Soy Tu Profe
matemáticas - geometría del espacio - sólidos geométricos - pirámide - el profesor Ayala explica la resolución de preguntas de volumen de un tronco de pir. Aprovechando la función definida en el apartado anterior (demostración del área), podemos calcular el volumen del tronco de cono como cuerpo de revolución: El cuadrado de la función f f es. Calculamos la integral: Recordad que r = R2 − R1 r = R 2 − R 1, así que. Por tanto, el volumen del tronco de cono es.




