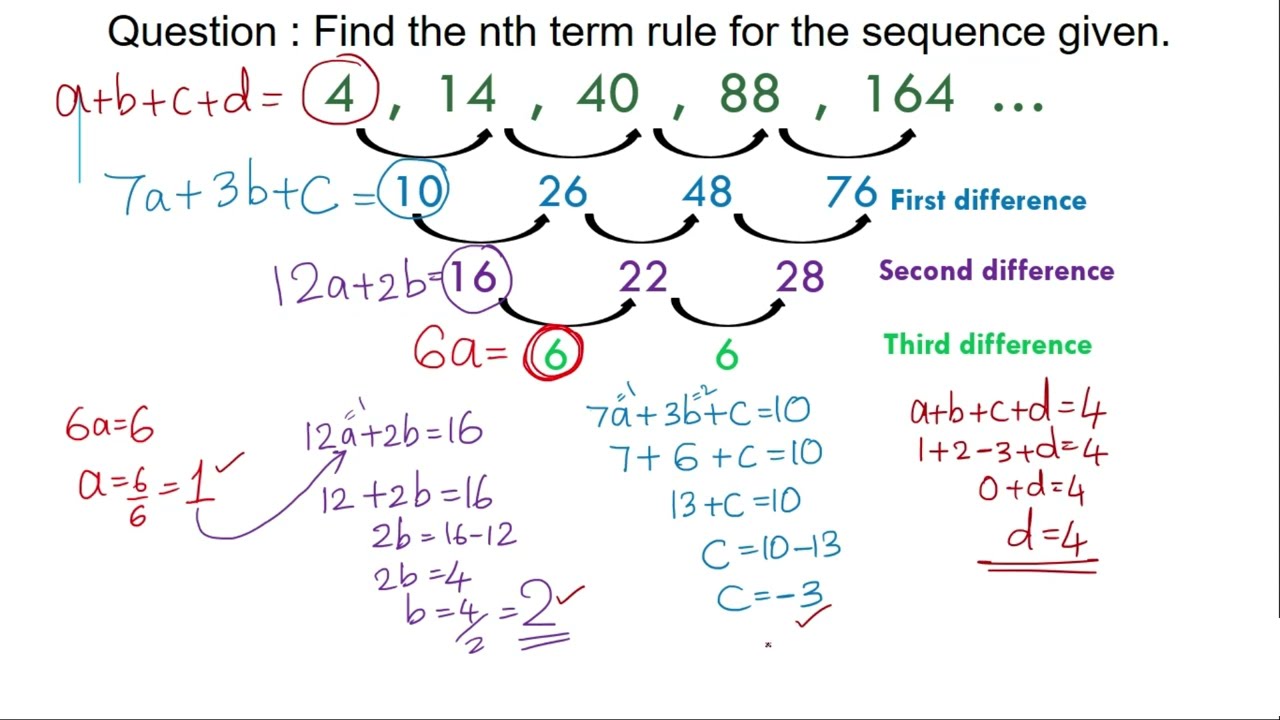
Cubic Sequences (Difference Method for the nth n th term) Cubic sequences are characterized by the fact that the third difference between its terms is constant. For example, consider the sequence : 4, 14, 40, 88, 164,. 4, 14, 40, 88, 164,. looking at the first, second and third difference of this sequence would look like : Quadratic And Cubic Sequences A series of free, online lessons suitable for GCSE Maths, with videos, examples and solutions. These lessons cover quadratic sequences and cubic sequences. Share this page to Google Classroom Related Pages Number Sequences Arithmetic Sequences Geometric Sequences Lessons for GCSE/IGCSE Maths
Cubic SequenceFinding the nth Term Formula YouTube
Cubic Sequences, how to find the formula for the n-th term, using the difference method.Cubic sequences of numbers are characterized by the fact that the thi. Cubic Sequences - Finding the nth Term Formula Kawthar Ali 2.27K subscribers Subscribe Subscribed 22K views 3 years ago IGCSE Extended Going through the process of finding the nth term formula. 1 {22, 15, 10, 7, 6, 7, . . . } A) . 8 sequence. Finally, find t cubic, or neither. Then find the equation of each Determine if each sequence is arithmetic, quadratic, Example: + cn + d 2 + bn 3 Its equation has the form tn = an • Common Difference occurs at D3 • A Cubic Sequence Cubic Sequences Section 1.5: Back In this lesson, we will investigate how terms change when a sequence is quadratic. In other words, it is of the form ax² + bx + c. We will also investigate cubic sequences.

Cubic Sequences How To Find Out The First 3 Numbers Of The Sequence
Level 4 - Quadratic sequence problem solving. Level 5 - Cubic sequences of the form an 3 + bn 2 + cn + d. Exam Style questions are in the style of GCSE exam paper questions and worked solutions are available for Transum subscribers. Handshakes - Try this lesson Starter which can generate a quadratic number sequence. I will be teaching you how to find the nth term expression for a Cubic Sequence using the formula and using trial and error method. Facebook-https: //web.fac. Cubic Sequences To find the n th term of a cubic sequence we will need to find the first, second and third differences. Similar to a quadratic sequence you then subtract an^3 from your original sequence, leaving you with a quadratic sequence, where you then follow the same steps as above to find the n th term. Example: General Term for Cubic Sequences. On this page there are videos explaining how to find the general or nth term of a cubic sequence. In this video we look at how to use the difference method to find the general term of a cubic sequence. You should make sure you are confident with quadratic sequences before watching this. In this method we look.

Cubic sequences YouTube
Cubic Sequences Worksheet 1 Try answering each of the following without a calculator. Show all of your working and state any formula used. Click on the link in the Header of this page, or scan the QR Code to view the online notes and tutorial(s) for this worksheet. Exercise 1 Since the first differences are the same, this means that the rule is a linear polynomial, something of the form y = an + b. I will plug in the first couple of values from the sequence, and solve for the coefficients of the polynomial: 1 a + b = 5. 2 a + b = 7. This system solves as: So the formula is y = 2n + 3.
The cubic formula is the closed-form solution for a cubic equation, i.e., the roots of a cubic polynomial . A general cubic equation is of the form (1) (the coefficient of may be taken as 1 without loss of generality by dividing the entire equation through by ). (a) Find the next three terms. Looking at the difference between the terms, we see that they are all 2. So this is a linear sequence with common difference 2 So the next three terms are 13 + 2 = 15 15 + 2 = 17

Quadratic and Cubic Sequences (solutions, examples, videos, worksheets
#Olevel #IGCSE #GCEOlevel #igcsemaths #numbersequence In this video, we will learn how to find the general term of a cubic sequenceLink to Livestream Mentio. A cubic number is a figurate number of the form with a positive integer. The first few are 1, 8, 27, 64, 125, 216, 343,. (OEIS A000578 ). The protagonist Christopher in the novel The Curious Incident of the Dog in the Night-Time recites the cubic numbers to calm himself and prevent himself from wanting to hit someone (Haddon 2003, p. 213).




