I segmenti notevoli del triangolo sono particolari tipi di segmentiche mettono in relazione vertici, angoli e lati di un triangoloqualsiasi. A seconda del tipo di relazione considerata possiamo parlare di altezza, bisettrice, medianae asse. L'altezza relativa alla base è anche mediana e asse relativo alla base, e bisettrice dell'angolo al vertice (cfr: altezza, mediana, bisettrice e asse ). Un triangolo equilatero è anche isoscele, ma un triangolo isoscele non è necessariamente equilatero.
Problema di Geometria Triangolo isoscele 4 La risposta che cerchi
In geometry, an isosceles triangle (/ aɪ ˈ s ɒ s ə l iː z /) is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case.Examples of isosceles triangles include the isosceles right triangle. Le tre mediane di un triangolo si incontrano sempre in un punto nel centro del triangolo. Se il triangolo è equilatero tutti i lati sono uguali e tutte le mediane sono di uguale lunghezza. Se. Immaginiamo dunque di disegnare un triangolo qualsiasi ABC con base AB e vertice C. Facciamo partire dal vertice C un segmento che termina nel punto medio del lato AB, che chiamiamo H. Il. Triangoli Mediana e baricentro. Primo e secondo criterio di congruenza dei triangoli. Teorema: "Un triangolo isoscele ha gli angoli alla base congruenti"🍀.

Whats a isosceles triangle lopeztk
Triangoli. TERZO criterio di congruenza. Nei triangoli isosceli: altezza=mediana=bisettrice Mario Antonuzzi 31.6K subscribers Subscribe Subscribed L i k e Share Save 3.8K views 11 years ago. Nei triangoli isosceli: la bisettrice dell'angolo al vertice è anche mediana e altezza. Il triangolo isoscele è un tipo di triangolo che ha due lati congruenti, ossia della stessa lunghezza, chiamati lati isosceli o lati obliqui. Il terzo lato del triangolo isoscele è la base del triangolo. I due lati congruenti creano due angoli alla base che sono anch'essi uguali o congruenti. In un triangolo isoscele gli angoli alla base sono congruenti. Ipotesi: Tesi: Dimostrazione Tracciamo la bisettrice dell'angolo in . I triangolo e sono congruenti per il primo criterio, infatti hanno: per ipotesi lato in comune perché è la bisettrice dell'angoloin .
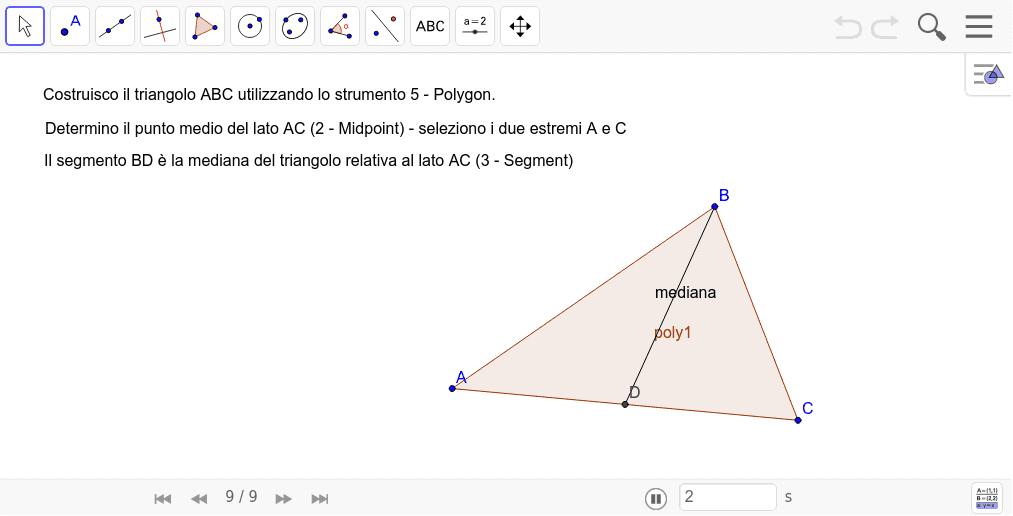
Mediana di un triangolo GeoGebra
Triangolo isoscele: definizione e formule dirette e inverse del triangolo isoscele. Teoremi completi di ipotesi, tesi e dimostrazione Disegniamo il TRIANGOLO ISOSCELE ricordando che esso è un triangolo i cui LATI OBLIQUI e i cui ANGOLI ALLA BASE sono CONGRUENTI: Ora disegniamo l' ALTEZZA relativa alla base e la chiamiamo A H: Ora ritagliamo il nostro triangolo e pieghiamo la figura lungo la linea dell'altezza, avremo: Notiamo che le due parti del triangolo coincidono.
Definiamo altezza di un triangolo il segmento di perpendicolare condotto da un vertice al lato opposto. In figura AH e' un'altezza. Naturalmente nel triangolo vi saranno tre altezze. Definiamo mediana il segmento congiungente il vertice di un triangolo con il punto medio del lato opposto. In figura AM e' una mediana. Se un triangolo è isoscele, allora la bisettrice dell'angolo al vertice è anche altezza e mediana rispetto alla base.link a geogebra: https://ggbm.at/DVcUnx5.

La bisettrice nel triangolo isoscele YouTube
La bisettrice di un triangolo isoscele relativa all'angolo al vertice coincide con altezza, mediana e asse relativi alla base. Ci sono alcuni triangoli che si possono considerare triangoli isosceli particolari. Essi sono: triangoli equilateri, triangoli rettangoli isosceli. Esistono anche triangoli isosceli ottusangoli e acutangoli. In un triangolo isoscele il segmento che unisce il vertice opposto alla base è contemporaneamente altezza relativa ad essa, mediana sempre della base, e bisettrice dell'angolo da cui ha origine.




