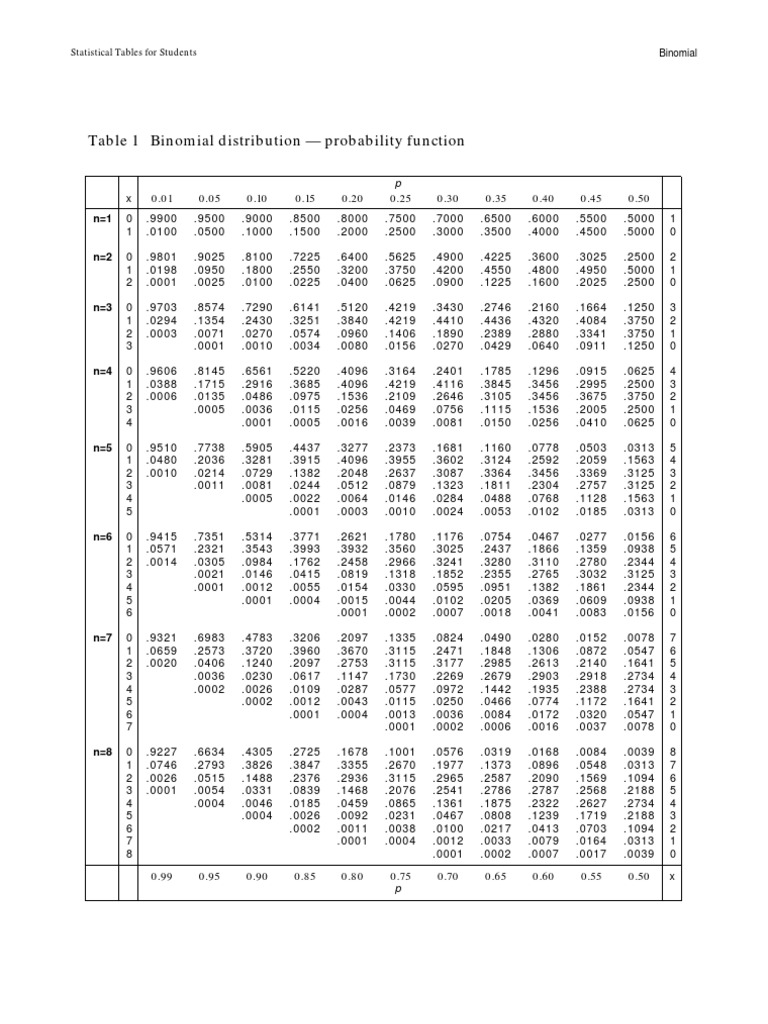
This binomial distribution table has the most common cumulative probabilities listed for n. Homework or test problems with binomial distributions should give you a number of trials, called n. Click the link below that corresponds to the n from your problem to take you to the correct table, or scroll down to find the n you need. n = 3: n = 4: Statistical Tables for Students Binomial Table 1 Binomial distribution — probability function p x 0.01 0.05 0.10 0.15 0.20 0.25 .300.35 .400.45 0.50

How To Use Binomial Probability Table Riviera Youlat
Table 4 Binomial Probability Distribution Table 4 Binomial Probability Distribution C p r qn − r n, r This table shows the probability of r successes in n independent trials, each with probability of success p. n r .01 .05 2 0 .980 .020 .000 0 .970 .029 .000 .000 0 .961 .039 .001 .000 .000 0 .951 .048 .001 .000 .000 .000 0 .941 .057 .001 .000 .000 The binomial distribution table is a table that shows probabilities associated with the binomial distribution. To use the binomial distribution table, you only need three values: n: the number of trials r: the number of "successes" during n trials p: the probability of success on a given trial In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments,. In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. Binomial Probability Distribution Table This table shows the probability of x successes in n independent trials, each with probability of success p . n x 2 0.01 0.9801 1 0.0198 2 0.0001 3 0.9703 1 0.0294 2 0.0003 3 4 0.9606 1 0.0388 2 0.0006 3 0.05 0.9025 0.0950 0.0025 0.8574 0.1354 0.0071 0.0001 0.8145 0.1715 0.0135
Binomial Table PDF
Binomial Distribution Table p n x 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.95 1 2 In general, the mean of a binomial distribution with parameters N (the number of trials) and π (the probability of success on each trial) is: (5.7.11) μ = N π. where μ is the mean of the binomial distribution. The variance of the binomial distribution is: (5.7.12) σ 2 = N π ( 1 − π) To learn how to determine binomial probabilities using a standard cumulative binomial probability table when p is greater than 0.5. To understand the effect on the parameters n and p on the shape of a binomial distribution. To derive formulas for the mean and variance of a binomial random variable. To understand the steps involved in each of. The outcomes of a binomial experiment fit a binomial probability distribution. The random variable X = the number of successes obtained in the n independent trials. The mean, μ, and variance, σ2, for the binomial probability distribution are μ = np and σ2 = npq. The standard deviation, σ, is then σ = npq−−−√ n p q.
Peter's Statistics Crash Course
To learn how to determine binomial probabilities using a standard cumulative binomial probability table when \(p\) is greater than 0.5. To understand the effect on the parameters \(n\) and \(p\) on the shape of a binomial distribution. This is a binomial problem because there is only a success or a failure, and there are a definite number of trials. The probability of a success stays the same for each trial. Notation for the Binomial: B = B = Binomial Probability Distribution Function. X ∼ B(n, p) (4.4.4) (4.4.4) X ∼ B ( n, p)
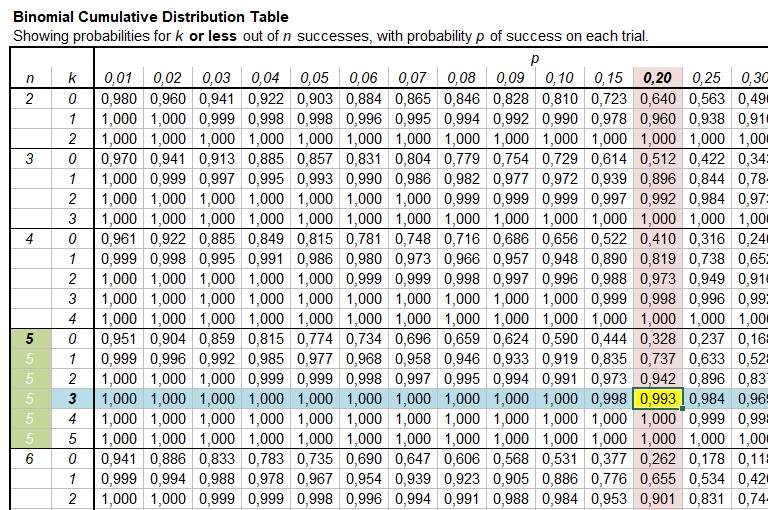
The variance of this binomial distribution is equal to np(1-p) = 20 × 0.5 × (1-0.5) = 5. Take the square root of the variance, and you get the standard deviation of the binomial distribution, 2.24. Accordingly, the typical results of such an experiment will deviate from its mean value by around 2. Using Binomial Tables Even for a relatively small value of n, the computation of binomial probabilities can be tedious. Appendix Table A.1 tabulates the cdf F(x) = P(X x) for n = 5, 10, 15, 20, 25 in combination with selected values of p. Various other probabilities can then be calculated using the proposition on cdf's.

Peter's Statistics Crash Course
The probability distribution of a binomial random variable is called a binomial distribution . Suppose we flip a coin two times and count the number of heads (successes). The binomial random variable is the number of heads, which can take on values of 0, 1, or 2. The binomial distribution is presented below. 0.50. The distribution of this type of variable, referred to as the binomial distribution, is completely determined by two parameters: n and p. Here n is the number of trials and p is the probability of success. The tables below are for n = 2, 3, 4, 5 and 6. The probabilities in each are rounded to three decimal places.




