2 2 x 2. x tan 1 ( ) 5. Table of Fourier Transform Pairs. Function, f(t) Fourier Transform, F(. ) Definition of Inverse Fourier Transform. Signals & Systems - Reference Tables 1 Table of Fourier Transform Pairs Function, f(t) Fourier Transform, F( ) Definition of Inverse Fourier Transform

Table of Fourier Transform Pairs Vidyarthiplus (V+) Blog A Blog for Students
In physics, engineering and mathematics, the Fourier transform ( FT) is an integral transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex -valued function of frequency. Fourier Transform Table, Pairs & Properties Fourier Transform Pairs Using these functions and some Fourier Transform Properties (next page), we can derive the Fourier Transform of many other functions. Information at http://lpsa.swarthmore.edu/Fourier/Xforms/FXUseTables.html © 2015, Erik Cheever Fourier Transform Properties Symmetry Properties This section gives a list of Fourier Transform pairs. That is, we present several functions and there corresponding Fourier Transforms. The derivation can be found by selecting the image or the text below. For convenience, we use both common definitions of the Fourier Transform, using the (standard for this website) variable f, and the also. Table 1: Properties of the Continuous-Time Fourier Series +∞ +∞ x(t) = akejkω0t = akejk(2π/T)t k=−∞ X k=−∞ X ZT x(t)e−jkω0tdt = T ak = x(t)e−jk(2π/T)tdt ZT Property Periodic Signal Fourier Series Coefficients Linearity Time-Shifting Frequency-Shifting Conjugation Time Reversal Time Scaling Periodic Convolution Multiplication Differentiation

Fourier Transform Tables
Fourier Transform Table x()t X(f) X(ω) δ(t) 1 1 1 δ(f) 2(πδω) δ()tt. The Fourier transform of a function is implemented the Wolfram Language as FourierTransform [ f , x, k ], and different choices of and can be used by passing the optional FourierParameters-> a , b option. By default, the Wolfram Language takes FourierParameters as . Unfortunately, a number of other conventions are in widespread use. Fourier Transform Table UBC M267 Resources for 2005 F(t) F�(ω) Notes(0) f(t) �∞ −∞ f(t)e−iωtdt Definition. (1) 1 2π �∞ −∞ f�(ω)eiωtdω f�(ω) Inversion formula. (2) f�(−t) 2πf(ω) Duality property. (3) e−atu(t) 1 a+iω a constant, �e(a) > 0(4) First, modify the given pair to. j 2sgn( t ) ⇔ 1 ω by multiplying both sides by j/2. Then, use the duality function to show that 1 t ⇔ 2 π j 2sgn ( −ω ) = j π sgn ( −ω ) = − j π sgn ( ω ) . 4. Table of Fourier Transform Pairs of Energy Signals. Function.
Fourier series table
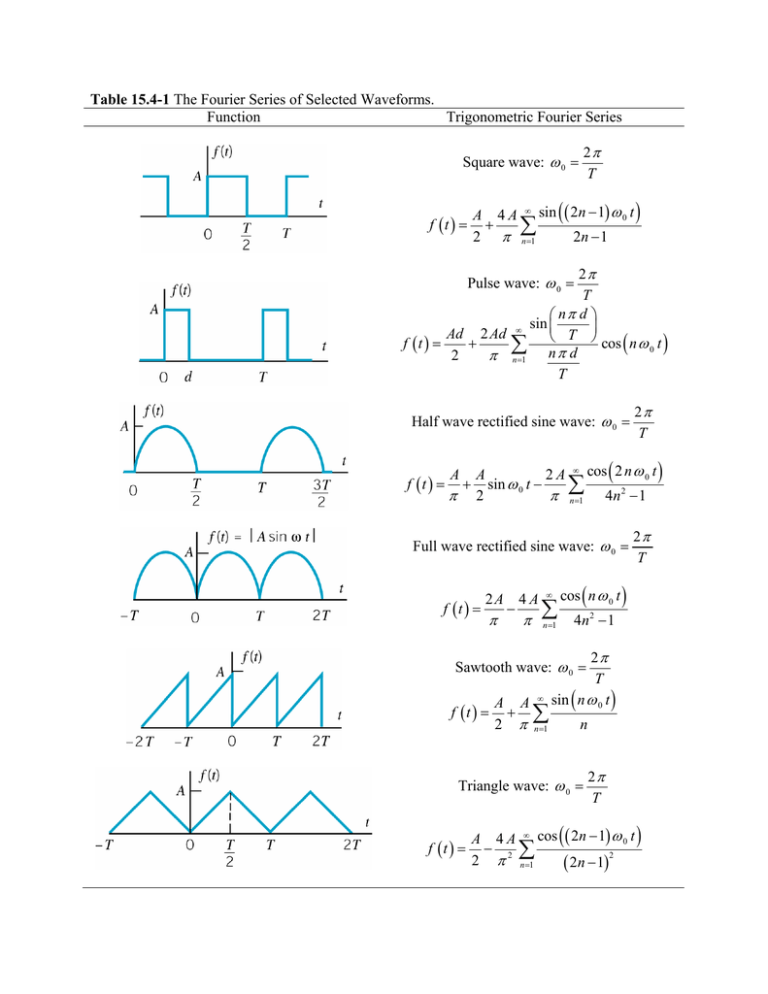
Fourier transforms 1 Strings To understand sound, we need to know more than just which notes are played - we need the shape of the notes. If a string were a pure infinitely thin oscillator, with no damping, it would produce pure notes. TABLE 4.2 BASIC FOURIER TRANSFORM PAIRS Signal :2: +oo akejkwof k=-00 '1.:rc-eiwot I()~ wo COS Wot sin wot x(t) = 1 Periodic square wave { 1, JtJ
7'1 sin Wt 7Tt o(t) u(t).
Formula (6) transforms into its Fourier transform, and (5) is the inverse transform. Related to this are the Fourier cosine transform (Sec. 11.8) (7) and the Fourier sine transform(Sec. 11.8) (8) . The discrete Fourier transform (DFT)and a practical method of computing it, called the fast Fourier transform (FFT), are discussed in Sec. 11.9. fˆ. If the signal is composed of two tones, then the Fourier transform will find those two tones. In vision, the Fourier transform is important because you can also use it to decompose two-dimensional images into "spatial frequency components". Variations in the brightness of the image that change slowly across the image, or ones that vary rapidly. 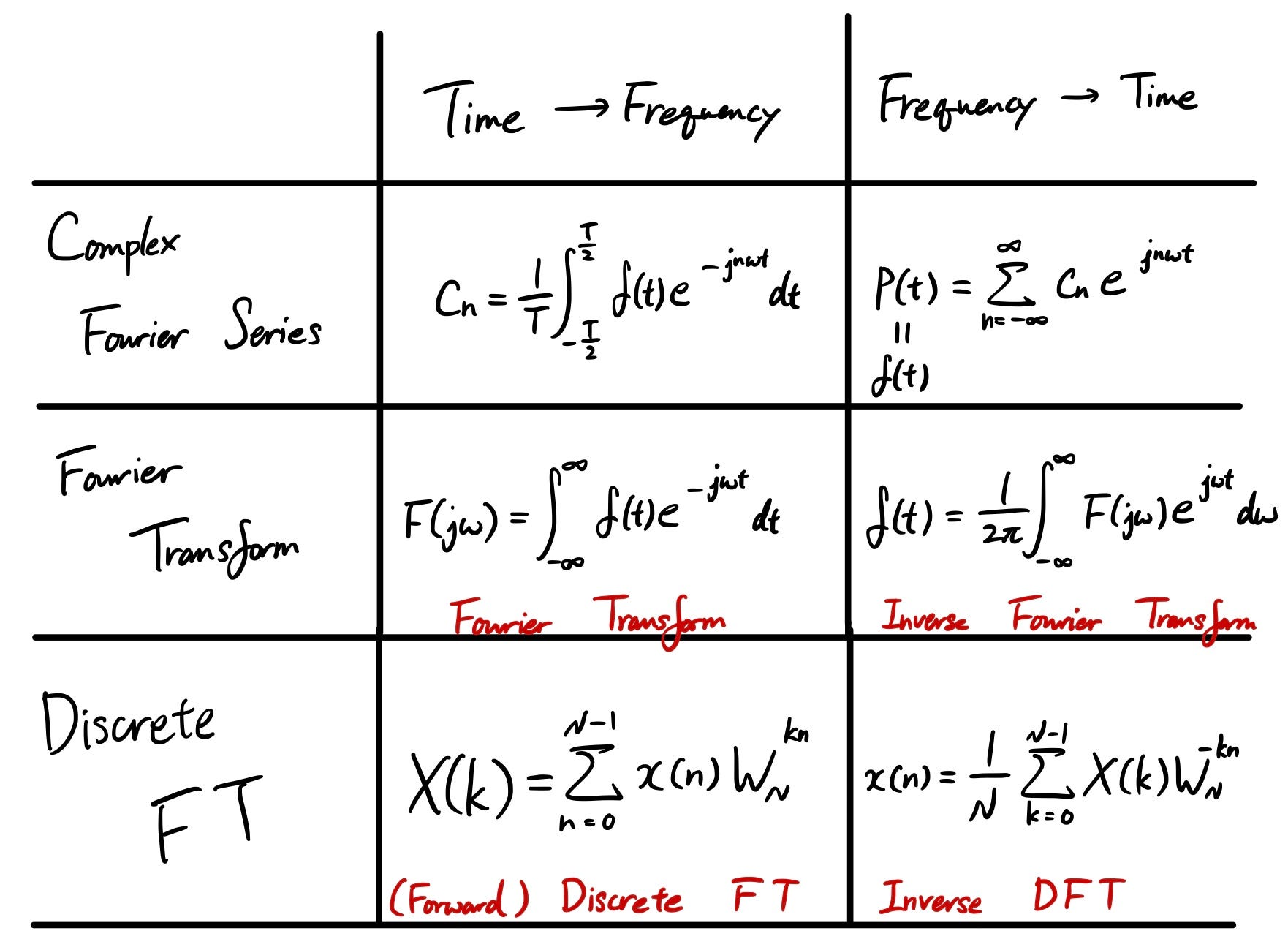
Fourier Transform 101 — Part 4 Discrete Fourier Transform by Sho Nakagome sho.jp Medium
Table of Fourier transforms; Table of Laplace transforms; Index; Get access. Share. Cite. Summary. A summary is not available for this content so a preview has been provided. Please use the Get access link above for information on how to access this content. Type Chapter Information The Fourier transform maps a function of time t to a complex-valued function of real-valued domain ω. Frequency plots provide intuition that is difficult to otherwise obtain. Find the Fourier transform of the following square pulse. X1(jω) = e ω 1 − e −ω 2. X1(jω) = sin ω ω ω. ω 2 X1(jω) = e − e −ω 4.




