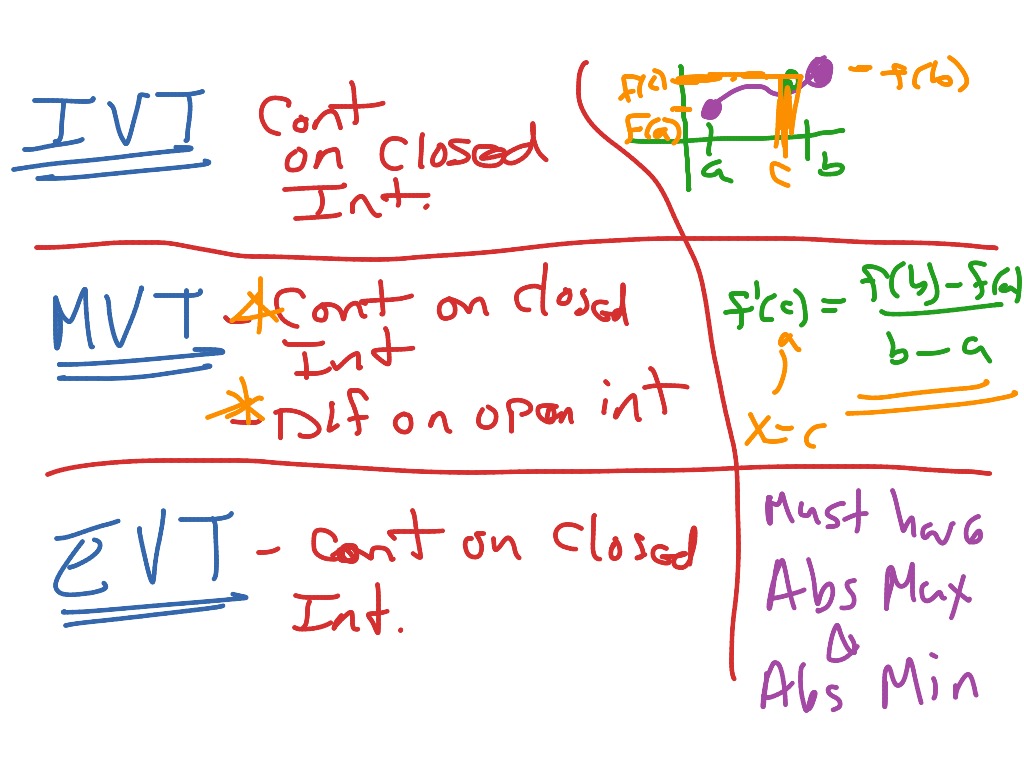
1 / 13 Flashcards Learn Test Match Q-Chat MrsGartnerGeom Teacher Top creator on Quizlet Students also viewed IVT, EVT, MVT, and Rolle's Theorem 12 terms AlaynaBinder Preview Unit 5 MCQ AP Calc AB 36 terms YaBoiTalal Preview Module 5 test 10 terms GrayTurtle84102 Preview Annexe CALCUL INTÉGRAL 69 terms quizlette27196176 Preview The mean value theorem (MVT) is an existence theorem similar the intermediate and extreme value theorems (IVT and EVT). Our goal is to understand the mean value theorem and know how to apply it. MVT and its conditions
️Ivt Mvt Evt Worksheet Free Download Gambr.co
In this video we go over three theorems you must know if you're taking the AP Calculus Exam (AB or BC) the Value Theorems: Extreme Value Theorem (EVT), Intermediate Value Theorem (IVT), and. According to the IVT, somewhere between -1 and 2, there will be someplace where f(c) = -2 (or -1, or -1⁄2.) When to use it: Use to prove that a particular intermediate y value when you know two other y values on a continuous function. NOT with derivatives!! MVT - Mean Value Theorem Study with Quizlet and memorize flashcards containing terms like Intermediate Value Theorem (IVT), Extreme Value Theorem (EVT), Mean Value Theorem (MVT) and more. Sam's Calculus Tutorials 46 subscribers 4 Share 235 views 2 years ago Calculus AB Today we're going to go over a few basic calculus theorems that can be used to prove various aspects regarding the.
IVT EVT MVT YouTube
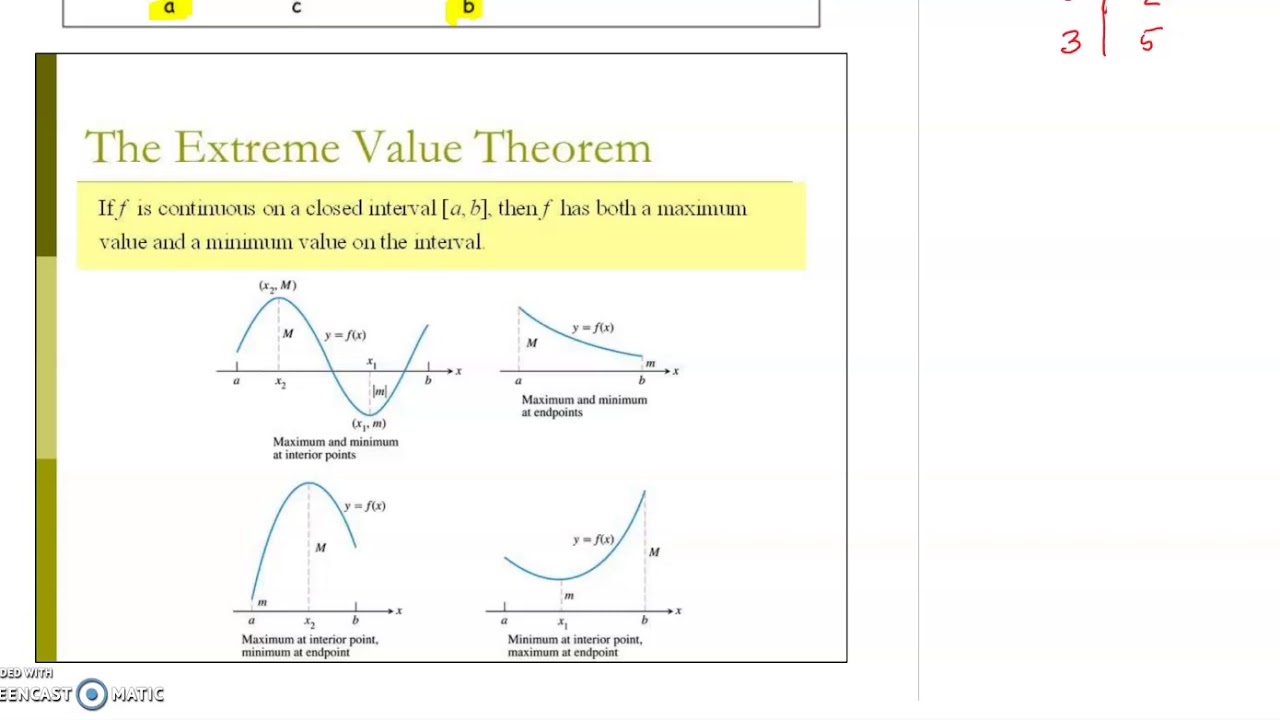
In this video, we look at an AP Calculus multiple choice question that deals with the Intermediate Value Theorem, Mean Value Theorem, and Extreme Value Theorem. Math 1A: Calculus Instructor: Alexander Paulin Handout: IVT, EVT, MVT Discussions 201, 203 // 2018-10-22 eorem (Intermediate Value eorem). Let a < b be real numbers and suppose f is a function that is on the (adjective) closed interval [a, b]. If d is any value strictly between and then there exists c in the interval (a, b) for which f (c) = d. The intermediate value theorem (IVT) and the extreme value theorem (EVT) are existence theorems. They guarantee that a certain type of point exists on a graph under certain conditions. Below is Isla's attempt to write a formal justification for the fact that the equation f ( x) = 200 has a solution where 0 ≤ x ≤ 5 . Is Isla's justification complete? If not, why? We are given that f is continuous. So, according to the intermediate value theorem, f ( x) = 200 must have a solution when x is between x = 0 and x = 5 .

4.14.6 Review Derivatives, MVT & IVT, Intervals of increase/decrease
When writing a justification using the IVT, you must state the function is continuous even if this information is provided in the question. MVT. If f (x ) is continuous on the. closed interval a, b and. differentiable on a, b , then there must exist at least one value c in a, b such that. What is the intermediate value theorem? The intermediate value theorem describes a key property of continuous functions: for any function f that's continuous over the interval [ a, b] , the function will take any value between f ( a) and f ( b) over the interval.
What is the Intermediate Value Theorem? Basically, it's the property of continuous functions that guarantees no gaps in the graph between two given points. In this article, what you need to know about Intermediate Value Theorem for the AP Calculus exams. The Intermediate Value Theorem (IVT) Here's the statement of the theorem: function k. Reach each explanation and decide whether you would apply IVT, EVT, or MVT. 17. Since k is differentiable, it is also continuous. Since k(6) — 2 and and since 1 is that k(c) = 1 for some c between 6 and 7. between 2 and 0, it follows by k(3)-k(2) , it 18. Since k is differentiable and, therefore, also continuous, and since 3-2

Mean Value Theorem (MVT) pg 5, pt 1 YouTube
Conditions for IVT and EVT: table. Google Classroom. 0 energy points. About About this video Transcript. Analyzing various conditions to see if the intermediate value theorem or extreme value theorem can be applied to a function, and analyzing a worked example of applying these theorems. Questions Tips & Thanks. This video covers Intermediate Value Theorem, Mean Value Theorem, and Rolle's Theorem. We also vaguely explain continuity and differentiabilty, and how they.




